Let (f in L^{2}left(mathbb{R}_{m}^{+} ight), g in L^{2}left(mathbb{R}_{n}^{+} ight))and assume that the functions are symmetric: (f=widehat{f}), (g=widehat{g}).

Let \(f \in L^{2}\left(\mathbb{R}_{m}^{+}\right), g \in L^{2}\left(\mathbb{R}_{n}^{+}\right)\)and assume that the functions are symmetric: \(f=\widehat{f}\), \(g=\widehat{g}\). We define the contraction as\[\begin{aligned}& \left(f \otimes_{r} g\right)\left(t_{1}, \ldots, t_{m-r}, s_{1}, \ldots, s_{n-r}\right) \\& :=\int \cdots \int_{\mathbb{R}_{+}^{r}} f\left(t_{1}, \ldots, t_{m-r}, u_{1}, \ldots, u_{r}\right)g\left(s_{1}, \ldots, s_{n-r}, u_{1}, \ldots, u_{r}\right) d u_{1} \ldots d u_{r}\end{aligned}\]

Show the following formula: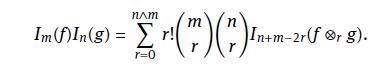

Consider first \(f=f_{1}^{\otimes m}\) and \(g=g_{1}^{\otimes n}\), use Theorem 20.13.i) and the relation between Hermite polynomials and iterated integrals.

Data From 20.13 Theorem 

Transcribed Image Text:

r! ((r) Int In+m-2rfor g). Im (f)In(g) = n^m T=0