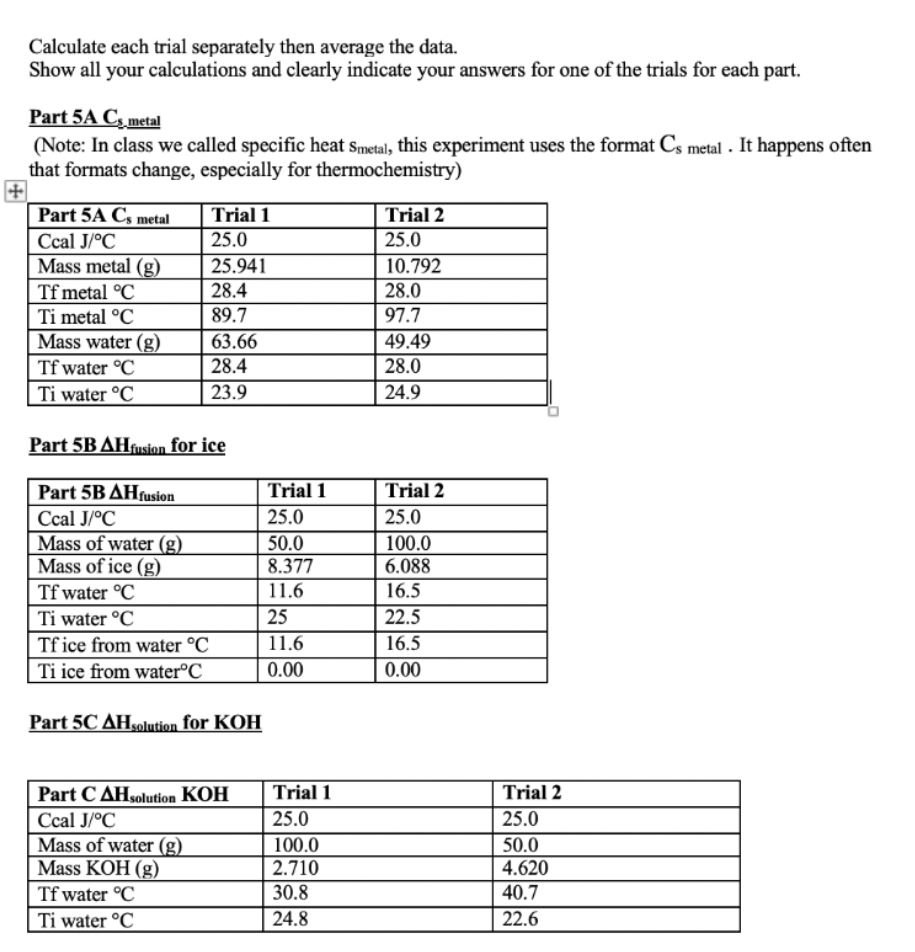
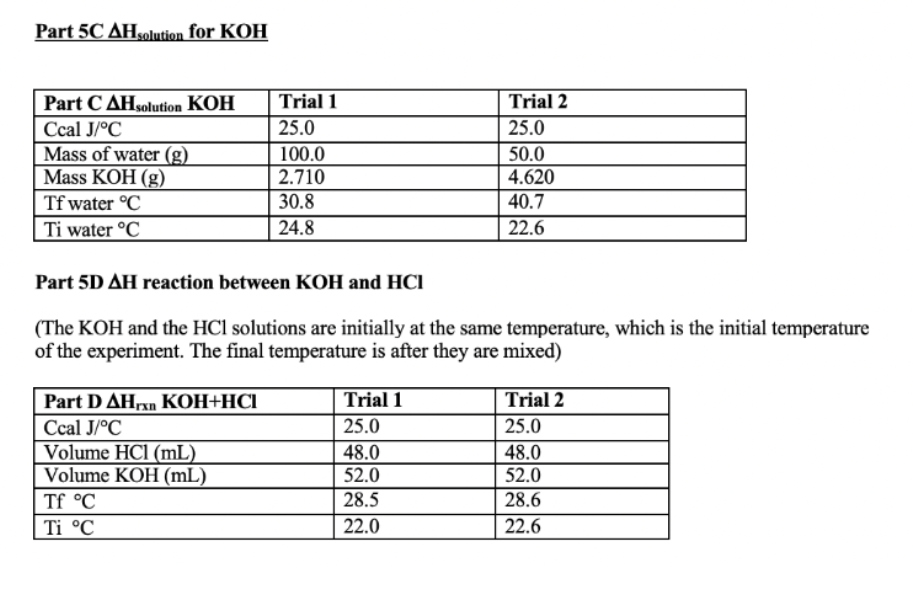
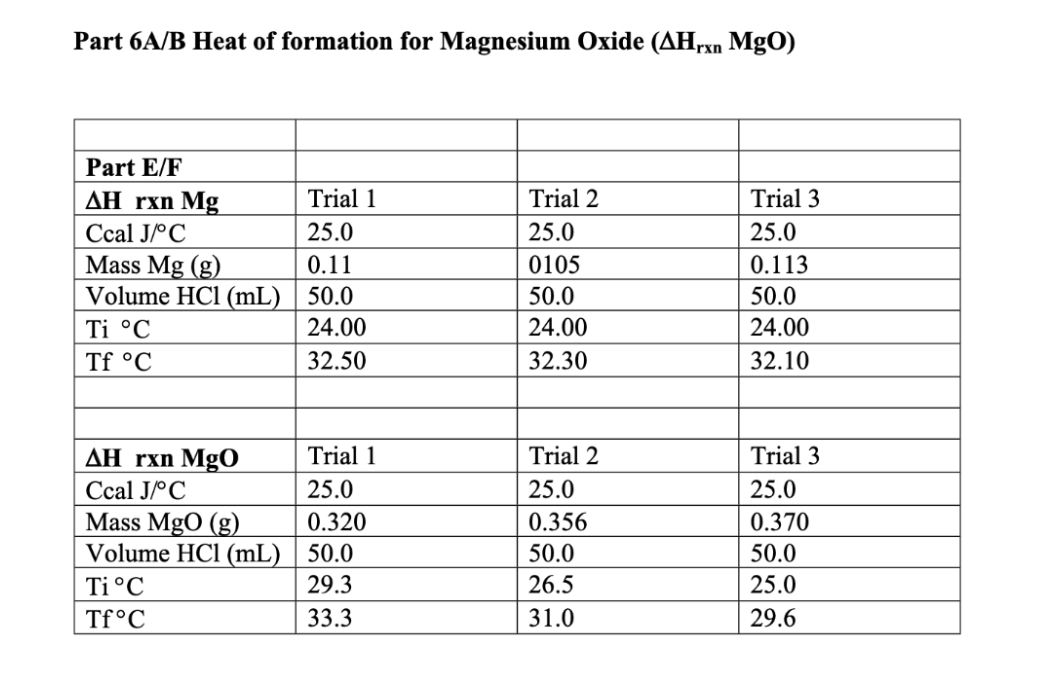
Calculate each trial separately then average the data. Show all your calculations and clearly indicate your answers for one of the trials for each part. Part 5A Cs metal (Note: In class we called specific heat Smetal, this experiment uses the format Cs metal . It happens often that formats change, especially for thermochemistry) Part 5A C, metal Ccal J/C Mass metal (g) Tf metal C Ti metal C Mass water (g) Tf water C Ti water C Trial 1 25.0 25.941 28.4 89.7 63.66 28.4 23.9 Trial 2 25.0 10.792 28.0 97.7 49.49 28.0 24.9 Part 5B AHfusion for ice Part 5B AHfusion Ccal J/C Mass of water (g) Mass of ice (g) Tf water C Ti water C Tf ice from water C Ti ice from waterC Trial 1 25.0 50.0 8.377 11.6 25 11.6 0.00 Trial 2 25.0 100.0 6.088 16.5 22.5 16.5 0.00 Part 5C AH solution for KOH Part C AHsolution KOH Ccal J/C Mass of water (g) Mass KOH (g) Tf water C Ti water C Trial 1 25.0 100.0 2.710 30.8 24.8 Trial 2 25.0 50.0 4.620 40.7 22.6 Part 5C AHsolution for KOH Part CAH solution KOH Ccal J/C Mass of water (g) Mass KOH (g) Tf water C Ti water C Trial 1 25.0 100.0 2.710 30.8 24.8 Trial 2 25.0 50.0 4.620 40.7 22.6 Part 5D AH reaction between KOH and HCI (The KOH and the HCl solutions are initially at the same temperature, which is the initial temperature of the experiment. The final temperature is after they are mixed) Part D AHKOH+HCI Ccal J/C Volume HCI (mL) Volume KOH (mL) Tf C Ti C Trial 1 25.0 48.0 52.0 28.5 22.0 Trial 2 25.0 48.0 52.0 28.6 22.6 5A. Determining heat capacity of a metal: In this part you will measure the specific heat of a metal by measuring how much heat is gained by the surroundings as that piece of metal emits heat. Combing equations (3) and (4) we get equation 5. (m x CS X AT).metal = -(m x Cs x AT)surroundings (5) The surroundings will be the coffee cup calorimeter containing a known amount of water. A Styrofoam coffee cup is a good insulator; so most of the heat should be transferred from the metal only into the water and not much heat should be lost to the coffee cup or the surrounding air. However, the Styrofoam coffee cup calorimeter isn't perfect and has a small heat capacity which was determined to be 25 J/C by previous experiments. Although this number is small, we have to consider it when we perform our calculations. As was just noted above the surroundings are actually both the water and the coffee cup. So expanding the surroundings to include both absorbers of heat yields (m x Cs x AT)metal=- [(m x Cs x AT)water + (C XAT)calorimeter] (6) C is the heat capacity of the calorimeter or 25 J/C. Notice how it is slightly different from specific heat: it is not mass dependent. Since the mass of the calorimeter doesn't change (you are using the same one the whole time, whereas the metal's mass or the water's mass may change), we can use heat capacity instead of specific heat. In the first experiment, you will determine the specific heat of a metal. In order to calculate Cs-metal (in equation 6), you will of course need to know all the other terms. You will have to determine the mass of the metal and water and you will also need to know the specific heat of water. For example, If you used 10.0 grams of copper and 75.0 grams of water, and knowing the specific heat of water (4.184J/8C) then, (10.0g x CSonetu * (Tzel metal - Tocial metal) =- [(75.0 g x 4.184 J/6Cx (Tural water - Tinicial water)) + (125/05(Tral cal Tinitial code] (7) Since the water and the coffee cup are both the surrounding their temperature will always be the same. That means, Atwater = Atsalecimeter 5B. Determining the heat of fusion of ice Next you will find the heat required to melt an ice cube. This number is called the molar enthalpy of fusion of ice (or the molar enthalpy of melting) and has symbol AHfusion. Remember that at constant pressure (like on a lab bench, where the atmospheric pressure is constant, and the system is not enclosed (like a bomb calorimeter]), enthalpy = heat (q = 4Hol, so the words heat and enthalpy are often used interchangeably (since we usually operate at constant pressure). When an ice cube melts, it is absorbing heat from the surroundings. That heat goes into not only into melting the ice cube, but also into warming the resulting water from ice to the temperature of the surroundings. (This analysis also assumes that the ice cube is at 0C, and not less than 0. If it were less that 0C, then first the ice has to warm to 0 before can it melts and so on...). The phase change from ice to water (melting) is a constant temperature process, meaning all the melting happens at 0C. The energy is going into the ice cube to separate the atoms (melt) rather than warm them up. Then once the ice cube is melted there is a puddle" of cold water that must absorb more energy to get to the final temperature of the surroundings. (So Tsion is the same for everything) Modifying equation (6) for this process gives Clest by surroundings = gained by ice cube to melt + Skalced by water from ice) (8) [(m x CS XAT) water + (C x AT)calorimeter] =- [( AHfusion X moles ice)+ (mice water X CSweter Atise water] (9) Some hints and questions: . The water in the calorimeter and the calorimeter both lose heat, that's why there are two terms on the left side of the equation. You should know all the values there. The mass of "water from ice" is the mass of the ice cube (the water came from the ice!) What is the initial temperature of the water from ice? (Once the ice melts, what temperature do you think the resulting water should be) The final temperature of the water in the calorimeter, the final temperature of the calorimeter and the final temperature of the water from ice is the same number (everything ends up at the same final temperature) You are trying to calculate the AHfusion Finally, in the last two parts of Experiment 5 you will measure the heat released when Part 5C: KOH(s) dissolves in water Part 5D: KOH reacts with HCI 5C. Determining heat of solution of KOH, AH solution: Heat of solution is the heat released or required when a solid dissolves in water, and it is reported as kJ/mole. KOH (s) has an exothermic heat of solution (some salts have endothermic heats of solution...can you think of one?). Again the same principles apply as in the previous parts of the experiment. The heat lost by the salt will be gained by the water and the calorimeter: (moles of KOH)| AH solution KOH) = -[(m x Cs x AT)water + (Cx AT)calorimeter] (10) Here you are solving for AHsolution KOH. 5D. Determining heat of reaction, AH xo: Similarly, when KOH and HCl react, it is an exothermic reaction. Ahora is the heat produced by the reaction, which is lost by the reaction into the water and the calorimeter. Since_glost = AHan (because we are at constant pressure in a coffee cup calorimeter), equation 10 can be rewritten as AH - [(m x Cs x AT)water + (C x AT)calorimeter) (11) Notice that equation 11 will give A Hor per total amount used and not per mole. In order to compare your determined value to the literature value, you must divide the SHoxe calculated by the moles of limiting reagent reacted (the reactant that runs out). Hint: you are using 50 mL each of a 1M solution. Experiment 6: Hess' Law and the Enthalpy of Formation of Magnesium Oxide The objective is to find the enthalpy of reaction for the formation of magnesium oxide. When magnesium is burned in oxygen, a large quantity of heat is released which results in a large, negative AHex Value: (Rxn A) Mg(s) + 1/2O2(g) Mgo(s) AHrxn = large negative number of joules, J The change in enthalpy of this reaction is quite difficult to measure directly by experiment and is beyond the scope of our lab set-up. However, the heat of reaction can be obtained indirectly by measuring the enthalpies of other reactions and using Hess' law. In accordance with Hess' Law, enthalpy changes for chemical reactions are additive. For example: We want to know what AHrxn** for the formation of NO (g) is from N2 and O2. But we are having trouble getting this reaction to occur. However, we can perform the following two reactions easily: N2(g)_+ 2O2(g) 2 NO2 (g) AH*rxn(2) = 66.4 kJ 2 NO(g)_+ O2(g) 2 NO2 (g) AHrxn(3) = - 114.1 kJ Using Hess' law, we can mathematically manipulate the reaction 2 and 3 and their AHrxn to calculate the AHrxn for our desired reaction. N2 (g) + 202 (g) + 2NO2 (g) AHrxn(2) = 66.4 kJ 2 NO2(g) 2 NO(g) + (8) - AHPrxn(3) =-(-114.1 kJ) = 114.1 kJ N2(g) + O2 (g) 2 NO(g) AHrxn(1) = 180.5 kJ or 90.3 kJ/mol We see that AH.(1), is equal to the sum of AH 80(2) and AH (3). Note that reaction 3 had to be used in reverse so the sign of the energy changed. This convention for the signs, positive or negative, of the enthalpy changes is important in order to obtain the correct answer when applying Hess' law. An exothermic reaction is one which releases energy and is assigned a negative value. An endothermic reaction is one which absorbs energy and is assigned a positive value. The additive property of His values will be applied in this experiment in order to determine the enthalpy change associated with the burning of magnesium metal in air. ** The symbol means the reaction was performed under standard conditions. You will see the symbol for the example because we are using literature values. When we perform our experiment, we won't be able to match standard conditions exactly, so our values will be slightly different than literature Hire values. For the combustion of magnesium, reaction (A) [top of page], one possible set of reactions is: (Rxn B) Mg(s) + 2 H+ Mg2( + H2(g) AH,xn(B) = negative number (experiment B5) (Rxn C) MgO 18 + 2 H+ (09 Mg2+ law + H2020 AH,x(C) = negative number (experiment B6) (Rxn D) % O2(g) + H2(g) H2O() AHxD) = -285.84 kJ/mol (heat of formation of water - can be looked up in your book) You will determine AH*rxn(B) and AHrxn(C) in experiment B5 and B6. You can then use the set of reactions B- D and their Hiss values to determine AH Ex(A). You will have to manipulate the reactions similar to the example for the formation of NO (g). 6A and 6B: Determining AH rxn: These two experiments will be very similar to experiment 5D, except we are adding a solid reactant to dilute acid. The general equation to calculate AH so will be the same: AH-[(mx Cs x AT)water + (C x AT)calorimeter] (11) To measure the AHar values for reactions (B) and (C) a small amount of each solid will be added to 100.0mL of HCI (our source for H+). The heat released by the reaction goes into the calorimeter. Using equation 11 the unit for this A Hoa will of course be in Joules (1). The AHa needs to be expressed as a "per mole" quantity. HCI will be used in excess, so the amount of solid will be the limiting reagent and the calculated AHag needs to be divided by the number of moles of the solid reacted. AHx/mole -- (Cswater * water. x ATwater Ccal X Alcal/moles; (12) Measuring AT Instead of a thermometer, a temperature probe interfaced to a computer will be used to acquire the temperature readings in this experiment. Because no calorimeter is free from heat leaks, it is possible that you will see some heat loss to the surroundings reflected in your data. Figure 2 shows a temperature vs. time plot for a calorimetric experiment in which the reaction was exothermic. After the initial sharp rise in temperature when the reaction has begun (at time of mixing, t = 0 seconds), the temperature begins to decrease due to heat loss from the calorimeter - this might be much smaller for your calorimeter. As the temperature equilibrium becomes complete, the loss becomes steady and the temperature decrease is linear. Figure 2: T (C) A linear fit of the temperature before and after the addition of the solid reactant will give T and Tf when we extrapolate the line to the y-axis. Ti t=0 Time (seconds) Procedure Experiment 6 The temperature will be monitored using the Logger Pro program. Plug the temperature probe into the Vernier box, which plugs into the computer. Turn on the computer and open Logger Pro. If the temperature probe is properly connected, you will see a screen labeled Temperature vs. time. The program is now ready for data acquisition. When you want to acquire data you click on the start button (green arrow). When you are finished collecting a data set, click stop (red square). You should be collecting data for the entire run for each trial. Your set-up is the same as it was for part A, except substitute the temperature probe for the thermometer. Repeat each run 2 times. For both reactions B and C, you will need to know the exact mass of HCl and Mg or Mgo. For reaction (B) you should use 100.0 mL of 1 M HCl and 0.07 g of Mg For reaction (C) you should use 100.0 mL of 1 M HCl and .25 g of Mgo . . Important Hints to perform the experiment: Set data collection to 30 min (it won't take that long, but you don't want the data collection to stop during the experiment). Make sure you collect a data point at least once every 10 seconds (6 or more data points per minute). Determine the mass of water (dilute HCI) as in previous experiments by difference. Make sure you record the precise mass of solid reactant. Start collecting data for about 1 minute to establish a straight baseline for your initial temperature before adding the solid reactant. Try to get as much of solid reactant into calorimeter as possible while continuing to collect data. Make sure you stir well, otherwise you will get a wavy plot and have to repeat the experiment. After the temperature has increased and starts to settle, try to get 1 minute worth of a fairly straight line. To determine T and Tt, you will have to fit the straight line before and after addition of the solid reactant using a linear fit. Try to get as small of a slope as possible - your y-intercept is your temperature reading. If you line is not horizontal you might introduce an error. Part 6A/B Heat of formation for Magnesium Oxide (AHrxn MgO) Part E/F AH rxn Mg Ccal J/C Mass Mg (g) Volume HCl (mL) Ti C Tf C Trial 1 25.0 0.11 50.0 24.00 32.50 Trial 2 25.0 0105 50.0 24.00 32.30 Trial 3 25.0 0.113 50.0 24.00 32.10 AH rxn Mgo Ccal JC Mass Mgo (g) Volume HCl (mL) Ti C TfC Trial 1 25.0 0.320 50.0 29.3 33.3 Trial 2 25.0 0.356 50.0 26.5 31.0 Trial 3 25.0 0.370 50.0 25.0 29.6 Calculations: Show a sample calculation for each experiment; show one average and % deviation calculation. Show each original formula with variables and with numbers substituted. (1) Csopetal (2) AHfusion of ice (3) AHsolution for KOH (4) AHreaction for KOH + HCI Calculate each trial separately, then average your results. The introduction to part A (pages 2-5) contains all the equations you need and gives you useful information for each calculation. Look up the literature (true) values for experiments A-D and calculate a percent deviation for those parts. For experiment C, you want to look for the heat of solution. For experiment D, you are looking for the enthalpy of neutralization. The net ionic reaction is H+ (aq) + OH+ (aq) H20 (1). You can use this to find the literature (true) value. Literature Values: Cs metal 0.900 J/C AH fusion of ice 6.02 kJ/mol AH solution for KOH -54.4 kJ/mol AH reaction for KOH + HCI -57.3 kJ/mol Look up the Heat of formation for Magnesium Oxide (DH4 Mgo) to calculate % error for experiment 6. (You only need a % error for the final calculation, the heat of formation of MgO; you do not need a % error for the individual steps) (5A) specific heat of a metal (Cs metal) (5B) heat of fusion of ice (AHfusionice) (5C) heat of solution of KOH (AH soln KOH) (5D) heat of reaction for HCI + KOH (AHrxn) (6A) heat of reaction for Mg + HCl (AHrxn) (6B) heat of reaction for MgO + HCl (AHrxn) After finding the values in experiment 6A and 6B, don't forget to calculate the heat of formation of Mgo using Hess' Law