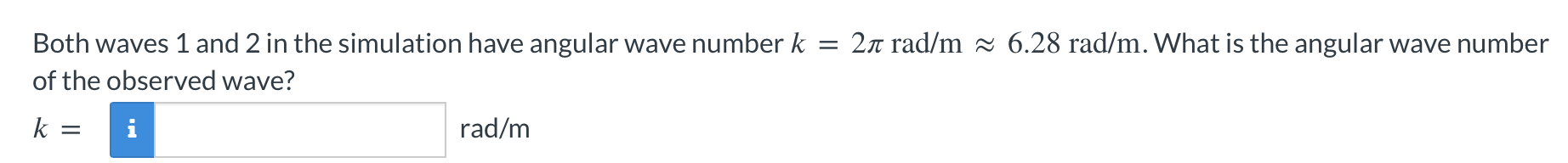
Consider two waves that travel in opposite directions along the same uniform rope. Suppose that two sinusoidal waves have the same amplitude ym, same angular wave number k, and same angular frequency @. Wave 2 has a phase shift & relative to wave 1, and wave 2 travels in the - x direction while wave 1 travels in the + x direction. When both waves exist simultaneously on the same rope, what kind of wave is observed? To answer this question, observe what is happening in the next simulation (linked below). The individual waves have displacements y and y2, respectively. The wave observed on the rope is the algebraic sum of the individual waves, Ynet = y + y2. Run the animation now. = Both waves 1 and 2 in the simulation have angular wave number k of the observed wave? k = i rad/m 2 rad/m 6.28 rad/m. What is the angular wave number The expression Ynet (x, t) = [2ym sin (kx)] cos (wt) gives the wave function for the net wave when the two waves travel in opposite directions with zero phase difference between them. What if the two waves are phase shifted relative to each other? For example, here are the wave functions for two waves to be combined: y(x, t) Ym sin (kx - wt) y(x, t) = ym sin (kx + wt + p) = The waves have the same angular wave number k, the same angular frequency w, and therefore the same speed. They travel in opposite directions, and wave 2 has phase shift & relative to wave 1. By applying the trigonometric identity from Module 16.5, - sin a + sin = 2 sin (a + ) cos (a B), you get the following expression for the resultant wave: rad 2)] cos (wt + 2/2) The amplitude of the resultant wave is given by the absolute value of the expression inside the square brackets: amplitude of resultant = 29,, sin (1 2ym kx + 9/-)1 Ynet (x, t) = 24m sin kx + We can use this expression for the amplitude to find the locations on the x axis where the resulting wave has nodes and antinodes. Suppose your goal is to obtain a resultant standing wave with a node located at x = 0.20 m. What value of in the range -T T will result in such a wave? (A)