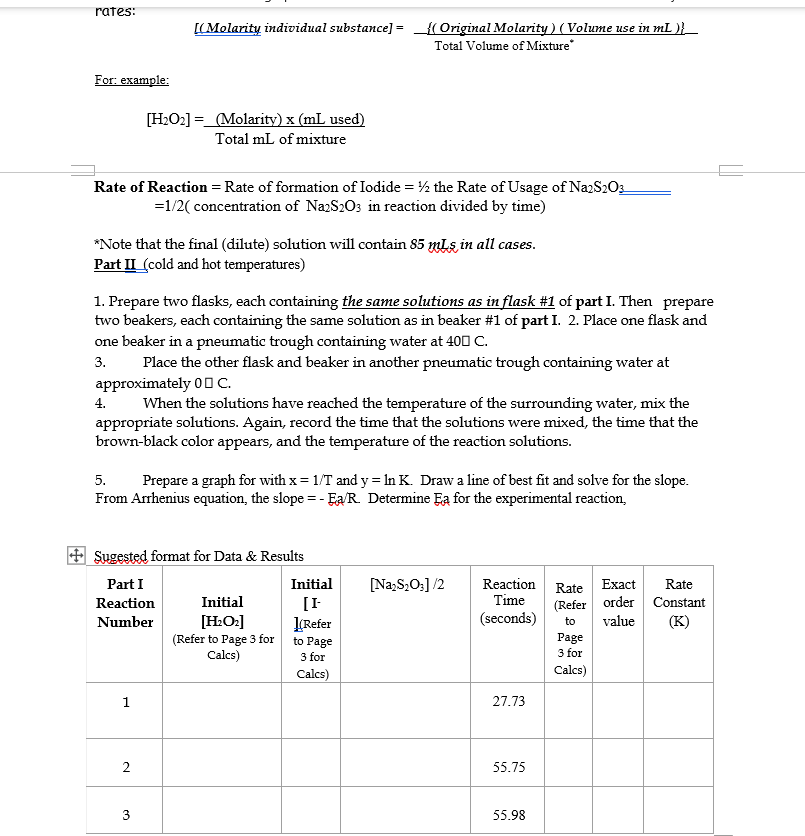
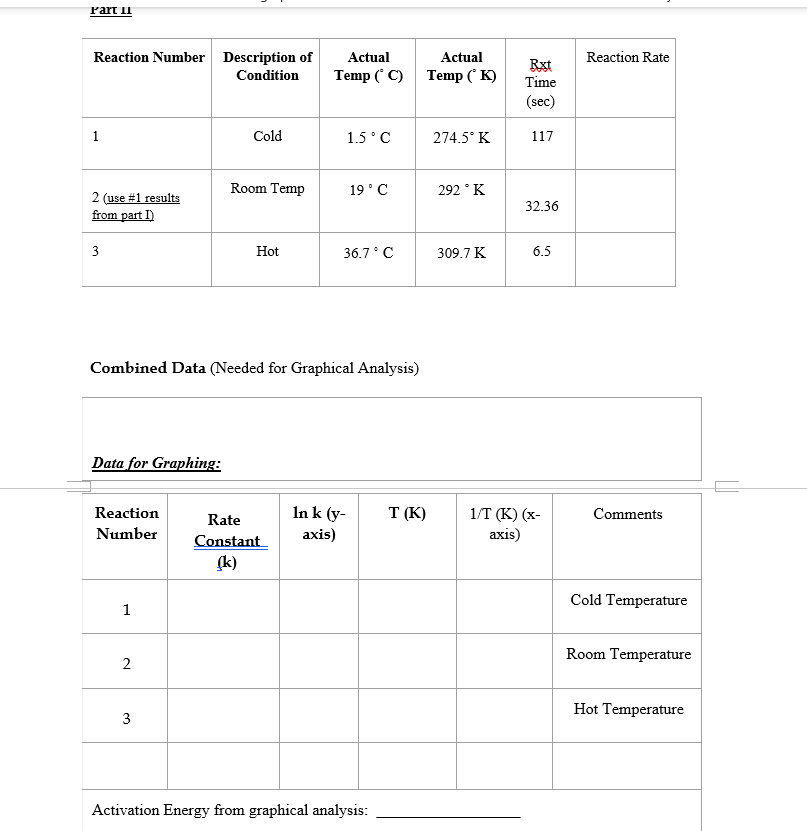
Experiment \#3 - Chemical Kinetics (using Iodine Clock Reaction) Objectives: Part I: To determine orders of reaction and rate constant, for the reaction of Iodide with Hydrogen Peroxide to produce Indine, and to write out the rate law. Part II: To demonstrate the applications of Arrhenius Equation and to determine the Activation Energy (Ea) using graphical analysis of results from Part I. Background/Concept (Supplement to topics learned in Lecture) The rate or speed of the reaction is dependent on the concentrations of iodide ion and hydrogen peroxide. Therefore, we can write a general rate equation for the reaction: Rate=k[I]a[H2O2]b (#2) Starch is added to the reaction mixture in order to calculate the rate of reaction. As iodine is formed during the reaction, it will immediately react with the starch to produce a complex with a brownblack color. This will tell you when the iodine is formed, but you have no idea as to the amount of hydrogen peroxide that has reacted in a.given amount of time, i.e., the rate of reaction. So, thiosulfate ion z is also added to the reaction mixture so that the following reaction will occur simultaneously with reaction (1). I2(qq)+2S2O32(gq)2I(qq)+S4O62(qq) (#3) Thus, the iodine that is formed in reaction (1) is immediately transformed into iodide ion and we do not see the blue-black color of the starch-iodide complex until all of the thiosulfate ion has reacted with I2(aa)). When this occurs, we will then know the amount of hydrogen peroxide that has reacted and the time it took to react. For example, if you start with 5.0105M of Na2S2O3 in the reaction flask and you see a color change after 20 seconds, then you can say that 2.5105M2 of I2 (a4) has been formed in 20 seconds and that 2.5x 105M of hydrogen peroxide has reacted in 20 seconds. [Remember for every 2 moles of thiosulfate ion reacting, only 1 mole of iodine and, therefore, 1 mole of hydrogen peroxide are reacting. This is the stoichiometric ratio from the two reaction equations, (3) and (1).] The rate of disappearance of hydrogen peroxide is 2.5105M divided by 20 seconds. This gives a value of 1.25106M/second. This is the value that will be recorded under REACTION RATE on the data sheet. Note that the concentration of the I((e) )ion doesn't change since it is regenerated in reaction (3). In all of the reactions the amount of thiosulfate ion used will be kept small relative to the amount of hydrogen peroxide. Therefore, the concentration of hydrogen peroxide will change very little and you will essentially be working with initial concentrations of reactants and initial rates of reaction. You will do a total of three reactions at room temperature, one reaction at cold temperature (about 5C ), and one reaction at hot temperature (about 40C, using a hot water bath). The three reactions at room temperature are labeled \#1,\#2 and \#3. These make up Part I of the experiment. For the reaction \#'s 1 and 2 the concentration of iodide is the same but the concentration of the other reactant, hydrogen peroxide, does vary. For the reaction \#'s 1 and 3 the concentration of experiment. For the reaction \#'s 1 and 2 the concentration of iodide is the same but the concentration of the other reactant, hydrogen peroxide, does vary. For the reaction \#'s 1 and 3 the concentration of hydrogen peroxide is the same but the concentration of the other reagent involved in the rate expression, the iodide ion, does vary. The amounts, and therefore the concentrations, of the starch, sulfuric acid, and sodium thiosulfate are constant for each reaction combination. In the reaction where the concentration of hydrogen peroxide (a molecular compound) is varied, the difference in the total volume of solution is compensated by the equivalent amount of another molecular compound water. In the reaction where the concentration of iodide ion is varied, the difference in total volume is compensated by the equivalent amount of another ion of the same charge the chloride ion. Effectively the total volume of the reaction, and the total ionic strength of the substances present is maintained at a constant value. After you have determined the reaction rate for each of the three reactions at room temperature you will substitute the values of the reaction rate, [I], and [H2O2] for reaction \#1 into equation (2). Then divide this entire equation by substituting the values for the reaction rate, [I], and [H2O2] for reaction \#2 into equation (2). This will give you a ratio of the reaction rates for reactions \#1 and \#2 on the left side; and a ratio of the products of k,[I]=a and [H2O2]b for reactions #1 and #2 on the right side. The values of k, and [I]l will cancel on the right side since they are the same for both reaction \#'s 1 and 2 . This gives you a number on the left equal to [H2O2]b/[H2O2]b on the right. The ratio on the right can be rewritten as {[H2O2]/[H2O2]b or a single number raised to the power " b ". The value of " b" can now be calculated. Now repeat the calculations for the two reactions where [H2O2] is kept constant and determine the value for "a". You can now calculate the value of "k" for each of the reactions since you have the values of "a" "b" , [I],[H2O2], and the reaction rate. The average of these three values is the value of "k" at room temperature. Part II The results of the three reactions run at different temperatures (cold, room temp and hot) make up Part II of the experiment. The mathematical relation, the Arrhenius equation, relates the rate constant k, and the temperature in the following equation: lnk=(Ea/R)(1/T)+lnA (H4) where Ea is the activation energy for the reaction, T is the temperature in Cs is the rate constant at T, and R is the ideal gas constant in units of J/molK and having a numerical value of 8.31. The equation is related to that of a straight line: y=mx+b. If "In k" is plotted against "l/T", then the slope of the resulting line will equal -Ea/R. The activation energy can be obtained by this method. LABORATORY PROCEDURE: Chemicals (Be aware of the actual concentrations used) Try to get only enough. Disposal: All mixtures should be poured into a Waste Bottle. NOTHING poured into the sink. (Pure/unused solutions should be properly returned) Procedures Part I (room temperatures) 1.) Label three clean and dry Erlenmeyer flasks from 1 to 3 . Do the same for three clean and dry beakers. Make up the solutions given below. Measure the solutions as accurately as possible by using graduated cylinders of the appropriate size. The graduated cylinder must be thoroughly rinsed before using with a separate solution. (Obtain and measure H2O2 when ready to mix; properly covered before pouring into the mixture). 2.) Add the contents of beaker \#1 to flask \#1. Immediately start your stopwatch as the two are added together. Continuously swirl the flask to mix the contents. When the solution turns (dark) bluelblack record the time and the temperature of the solution on the Data Sheet. Do exactly.the same for the remaining 2 pairs of solutions. If a beaker or a flask is to be reused it must be thoroughly rinsed with deionized water. The temperature of the reactions should remain within 1C of each other. The KCl solution is used so that the ionic strength of the various solutions may be kept at a fairly.constant level. On the Data Sheet, record the initial concentrations of hydrogen peroxide and iodide ions in the reaction solution. Remember that the original H2O2 and I solutions were diluted when they were mixed. together. For: example: [H2O2]=TotalmLofmixture(Molarity)(mLused) Rate of Reaction = Rate of formation of Iodide =1/2 the Rate of Usage of Na2S2O3 =1/2( concentration of Na2S2O3 in reaction divided by time) *Note that the final (dilute) solution will contain 85mLs in all cases. Part II (cold and hot temperatures) 1. Prepare two flasks, each containing the same solutions as in flask \#1 of part I. Then prepare two beakers, each containing the same solution as in beaker \#1 of part I. 2. Place one flask and one beaker in a pneumatic trough containing water at 40C. 3. Place the other flask and beaker in another pneumatic trough containing water at approximately 0CC. 4. When the solutions have reached the temperature of the surrounding water, mix the appropriate solutions. Again, record the time that the solutions were mixed, the time that the brown-black color appears, and the temperature of the reaction solutions. 5. Prepare a graph for with x=1/T and y=lnK. Draw a line of best fit and solve for the slope. From Arrhenius equation, the slope =Ea/R. Determine Ea for the experimental reaction, Combined Data (Needed for Graphical Analysis) Datafor Graphing: Activation Energy from graphical analysis: Experiment \#3 - Chemical Kinetics (using Iodine Clock Reaction) Objectives: Part I: To determine orders of reaction and rate constant, for the reaction of Iodide with Hydrogen Peroxide to produce Indine, and to write out the rate law. Part II: To demonstrate the applications of Arrhenius Equation and to determine the Activation Energy (Ea) using graphical analysis of results from Part I. Background/Concept (Supplement to topics learned in Lecture) The rate or speed of the reaction is dependent on the concentrations of iodide ion and hydrogen peroxide. Therefore, we can write a general rate equation for the reaction: Rate=k[I]a[H2O2]b (#2) Starch is added to the reaction mixture in order to calculate the rate of reaction. As iodine is formed during the reaction, it will immediately react with the starch to produce a complex with a brownblack color. This will tell you when the iodine is formed, but you have no idea as to the amount of hydrogen peroxide that has reacted in a.given amount of time, i.e., the rate of reaction. So, thiosulfate ion z is also added to the reaction mixture so that the following reaction will occur simultaneously with reaction (1). I2(qq)+2S2O32(gq)2I(qq)+S4O62(qq) (#3) Thus, the iodine that is formed in reaction (1) is immediately transformed into iodide ion and we do not see the blue-black color of the starch-iodide complex until all of the thiosulfate ion has reacted with I2(aa)). When this occurs, we will then know the amount of hydrogen peroxide that has reacted and the time it took to react. For example, if you start with 5.0105M of Na2S2O3 in the reaction flask and you see a color change after 20 seconds, then you can say that 2.5105M2 of I2 (a4) has been formed in 20 seconds and that 2.5x 105M of hydrogen peroxide has reacted in 20 seconds. [Remember for every 2 moles of thiosulfate ion reacting, only 1 mole of iodine and, therefore, 1 mole of hydrogen peroxide are reacting. This is the stoichiometric ratio from the two reaction equations, (3) and (1).] The rate of disappearance of hydrogen peroxide is 2.5105M divided by 20 seconds. This gives a value of 1.25106M/second. This is the value that will be recorded under REACTION RATE on the data sheet. Note that the concentration of the I((e) )ion doesn't change since it is regenerated in reaction (3). In all of the reactions the amount of thiosulfate ion used will be kept small relative to the amount of hydrogen peroxide. Therefore, the concentration of hydrogen peroxide will change very little and you will essentially be working with initial concentrations of reactants and initial rates of reaction. You will do a total of three reactions at room temperature, one reaction at cold temperature (about 5C ), and one reaction at hot temperature (about 40C, using a hot water bath). The three reactions at room temperature are labeled \#1,\#2 and \#3. These make up Part I of the experiment. For the reaction \#'s 1 and 2 the concentration of iodide is the same but the concentration of the other reactant, hydrogen peroxide, does vary. For the reaction \#'s 1 and 3 the concentration of experiment. For the reaction \#'s 1 and 2 the concentration of iodide is the same but the concentration of the other reactant, hydrogen peroxide, does vary. For the reaction \#'s 1 and 3 the concentration of hydrogen peroxide is the same but the concentration of the other reagent involved in the rate expression, the iodide ion, does vary. The amounts, and therefore the concentrations, of the starch, sulfuric acid, and sodium thiosulfate are constant for each reaction combination. In the reaction where the concentration of hydrogen peroxide (a molecular compound) is varied, the difference in the total volume of solution is compensated by the equivalent amount of another molecular compound water. In the reaction where the concentration of iodide ion is varied, the difference in total volume is compensated by the equivalent amount of another ion of the same charge the chloride ion. Effectively the total volume of the reaction, and the total ionic strength of the substances present is maintained at a constant value. After you have determined the reaction rate for each of the three reactions at room temperature you will substitute the values of the reaction rate, [I], and [H2O2] for reaction \#1 into equation (2). Then divide this entire equation by substituting the values for the reaction rate, [I], and [H2O2] for reaction \#2 into equation (2). This will give you a ratio of the reaction rates for reactions \#1 and \#2 on the left side; and a ratio of the products of k,[I]=a and [H2O2]b for reactions #1 and #2 on the right side. The values of k, and [I]l will cancel on the right side since they are the same for both reaction \#'s 1 and 2 . This gives you a number on the left equal to [H2O2]b/[H2O2]b on the right. The ratio on the right can be rewritten as {[H2O2]/[H2O2]b or a single number raised to the power " b ". The value of " b" can now be calculated. Now repeat the calculations for the two reactions where [H2O2] is kept constant and determine the value for "a". You can now calculate the value of "k" for each of the reactions since you have the values of "a" "b" , [I],[H2O2], and the reaction rate. The average of these three values is the value of "k" at room temperature. Part II The results of the three reactions run at different temperatures (cold, room temp and hot) make up Part II of the experiment. The mathematical relation, the Arrhenius equation, relates the rate constant k, and the temperature in the following equation: lnk=(Ea/R)(1/T)+lnA (H4) where Ea is the activation energy for the reaction, T is the temperature in Cs is the rate constant at T, and R is the ideal gas constant in units of J/molK and having a numerical value of 8.31. The equation is related to that of a straight line: y=mx+b. If "In k" is plotted against "l/T", then the slope of the resulting line will equal -Ea/R. The activation energy can be obtained by this method. LABORATORY PROCEDURE: Chemicals (Be aware of the actual concentrations used) Try to get only enough. Disposal: All mixtures should be poured into a Waste Bottle. NOTHING poured into the sink. (Pure/unused solutions should be properly returned) Procedures Part I (room temperatures) 1.) Label three clean and dry Erlenmeyer flasks from 1 to 3 . Do the same for three clean and dry beakers. Make up the solutions given below. Measure the solutions as accurately as possible by using graduated cylinders of the appropriate size. The graduated cylinder must be thoroughly rinsed before using with a separate solution. (Obtain and measure H2O2 when ready to mix; properly covered before pouring into the mixture). 2.) Add the contents of beaker \#1 to flask \#1. Immediately start your stopwatch as the two are added together. Continuously swirl the flask to mix the contents. When the solution turns (dark) bluelblack record the time and the temperature of the solution on the Data Sheet. Do exactly.the same for the remaining 2 pairs of solutions. If a beaker or a flask is to be reused it must be thoroughly rinsed with deionized water. The temperature of the reactions should remain within 1C of each other. The KCl solution is used so that the ionic strength of the various solutions may be kept at a fairly.constant level. On the Data Sheet, record the initial concentrations of hydrogen peroxide and iodide ions in the reaction solution. Remember that the original H2O2 and I solutions were diluted when they were mixed. together. For: example: [H2O2]=TotalmLofmixture(Molarity)(mLused) Rate of Reaction = Rate of formation of Iodide =1/2 the Rate of Usage of Na2S2O3 =1/2( concentration of Na2S2O3 in reaction divided by time) *Note that the final (dilute) solution will contain 85mLs in all cases. Part II (cold and hot temperatures) 1. Prepare two flasks, each containing the same solutions as in flask \#1 of part I. Then prepare two beakers, each containing the same solution as in beaker \#1 of part I. 2. Place one flask and one beaker in a pneumatic trough containing water at 40C. 3. Place the other flask and beaker in another pneumatic trough containing water at approximately 0CC. 4. When the solutions have reached the temperature of the surrounding water, mix the appropriate solutions. Again, record the time that the solutions were mixed, the time that the brown-black color appears, and the temperature of the reaction solutions. 5. Prepare a graph for with x=1/T and y=lnK. Draw a line of best fit and solve for the slope. From Arrhenius equation, the slope =Ea/R. Determine Ea for the experimental reaction, Combined Data (Needed for Graphical Analysis) Datafor Graphing: Activation Energy from graphical analysis