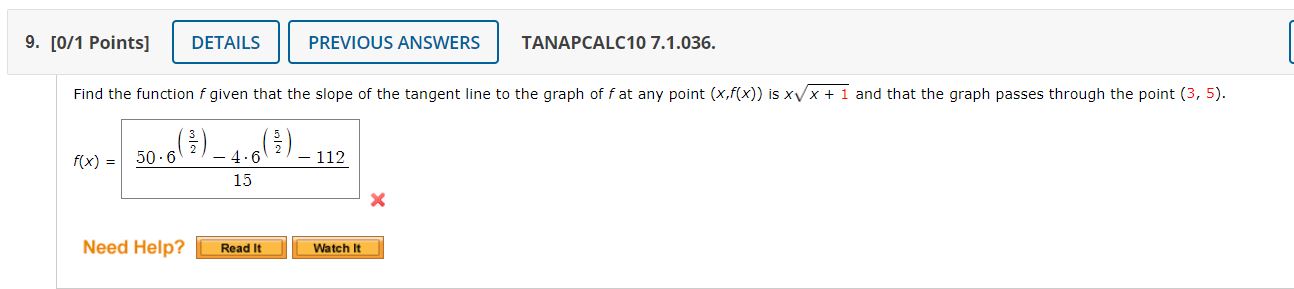
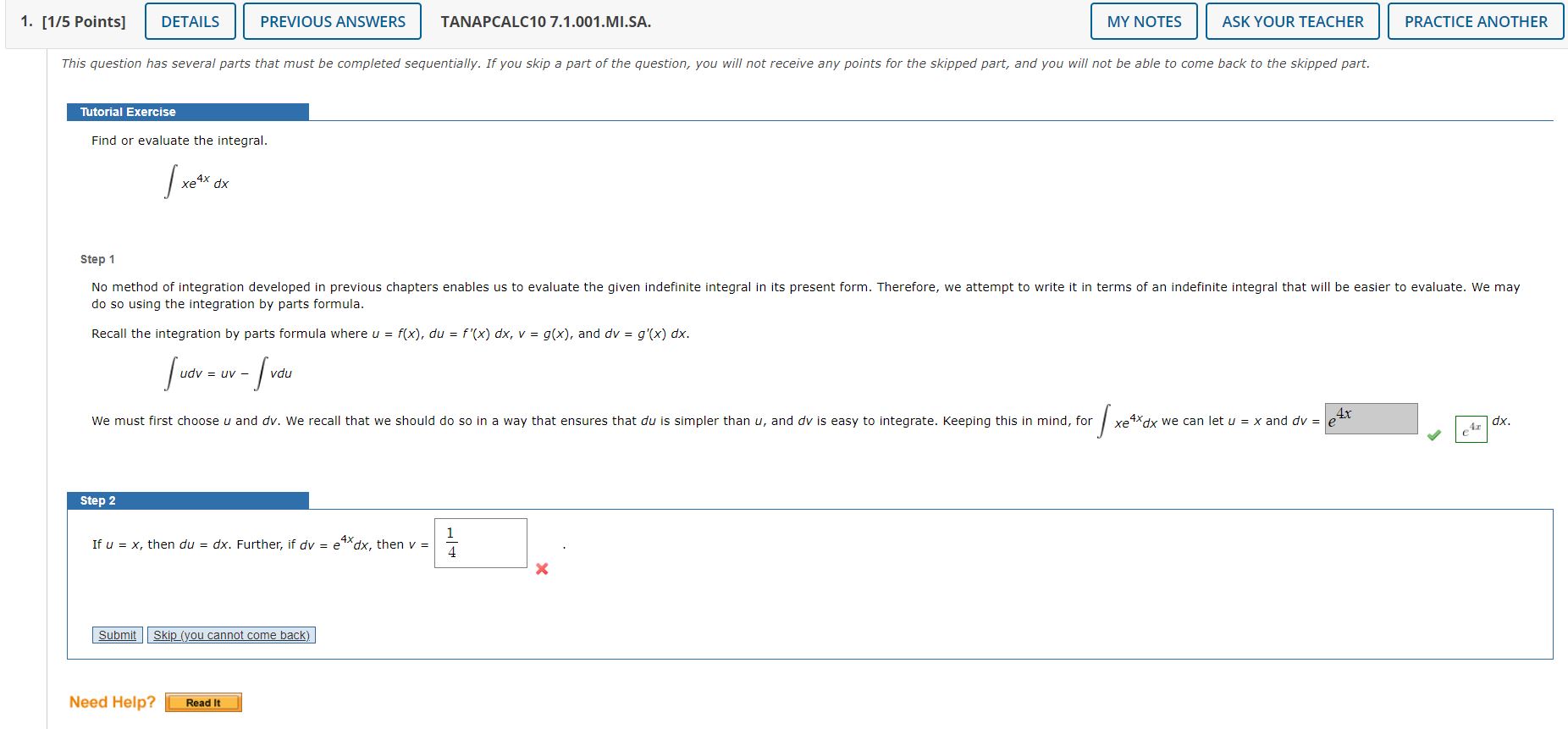
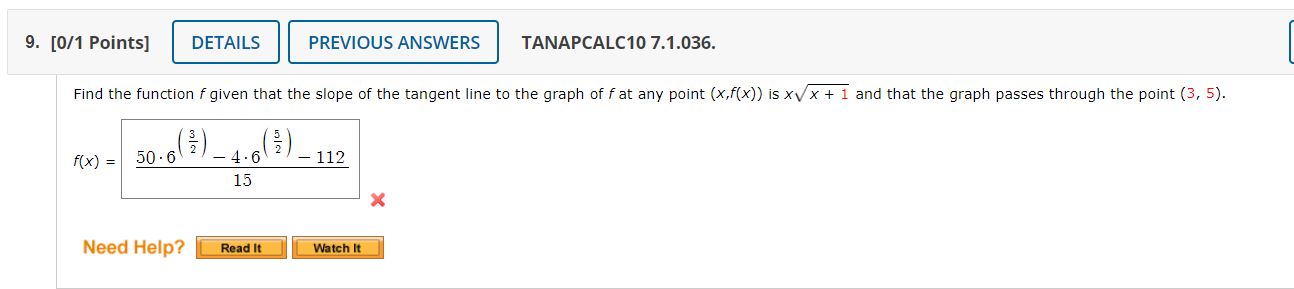
1. [1/5 Points] DETAILS PREVIOUS ANSWERS TANAPCALCIO 7.1 .OOI.MI.SA. This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. lutorial Exercise Find or evaluate the integral. xe x dx Step 1 No method of integration developed in previous chapters enables us to evaluate the given indefinite integral in its present form. Therefore, we attempt to write it in terms of an indefinite integral that will be easier to evaluate. We may do so using the integration by parts formula. Recall the integration by parts formula where u = f(x), du = f '(x) dx, v g(x), and dv g'(x) dx. udv = uv vdu We must first choose u and dv. We recall that we should do so in a way that ensures that du is simpler than u, and dv is easy to integrate. Keeping this in mind, for xe Xdx we can let u 4x x and dv dx. Step 2 If u x, then du dx. Further, if dv e 1 Xdx, then v 4 Need Help?