Let X and Y be two random variables with the joint probability density function: fxy(x,y) = e^-7, for 0

The marginal probability density function of X is expressed as fx(x) = e^-x, 0

- Find the marginal probability density function of Y.

- Find the conditional probability density function of Y given X.

- Are X and Y independent random variables?

: 1. Find the mean, variance, and standard deviation for the probability density function , f(x)=0.1,0?X?10.Graph the probability density function, then find and graph the cumulative distribution function on the same axes.

2. Find the mean, variance, and standard deviation for the probability density function f(x)=(1/2)e^(?x/2), 0?X Graph the probability density function, then find and graph the cumulative distribution function on the same axes.

3. Find the mean, variance, and standard deviation for the probability density function. ,f(x)=1.5x^2, ?1?X?1 Graph the probability density function, then find and graph the cumulative distribution function on the same axes.

For continuous random variables X and Y with joint probability density function ??(??, ??) = { ???? ?(??+????) ?? > 0 ?????? ?? > 0 0 ????????????????? a. Find ??(?? > 2 ?????? ?? > 1). b. Find the marginal probability density functions ????(??) and ????(??). c. Are X and Y independent? Explain. 8) Refer to Question 7. a. Find the conditional probability density function ????|??(??|2.5). b. Find the conditional probability density function ????|??(??|0.5). c. Find the conditional expectation ??(??|?? = 0.5)

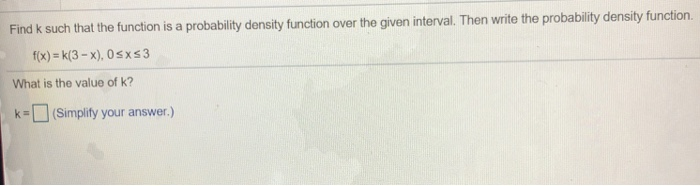
Find k such that the function is a probability density function over the given interval. Then write the probability density function. f(x) =k(3 - x). Osxs3 What is the value of k? k = (Simplify your answer.)