Shell Scripts

First, write a makefile for compiling the C source code files provided for the project (please see my web page given above). The generated executable should be named as cal.exe.

Note that you may face problems with the compilation of the code (the code is correct) and you need to figure out how to solve them. The code is correct and there is no need to change anything. When you compile each C source code file separately (you are required to do so in your makefile), you need to use proper options for gcc (or cc) to avoid complaints about undefined variables. Also, you need to figure out what other parts shall be included in the compilation command to properly compile the code without getting error messages.

Next, write a shell script exec.sh to compile the program using the make command and execute cal.exe with input from a file that you can call "cal.in" (Come up with your own input). In script exec.sh, you need to capture the output from cal.exe and print it to a file with name . In other words, your script needs to take as an input argument. Your shell script will need to execute cal.exe twice. In the second execution, you need to pipe the output of cal.exe to the wc command to f.

Find the programs below:

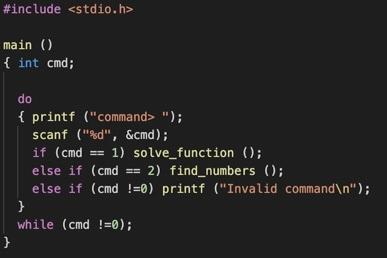
cal.c:

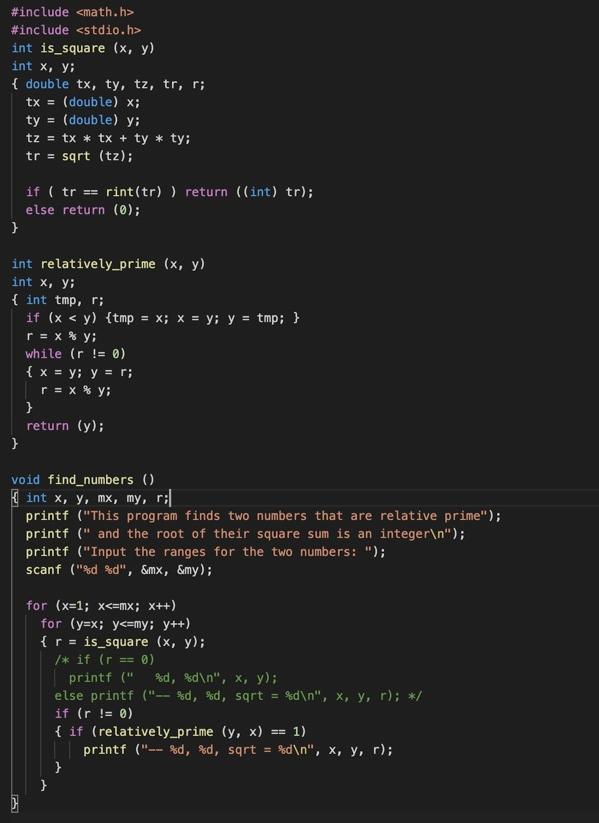
square.c:

quadratic.c:

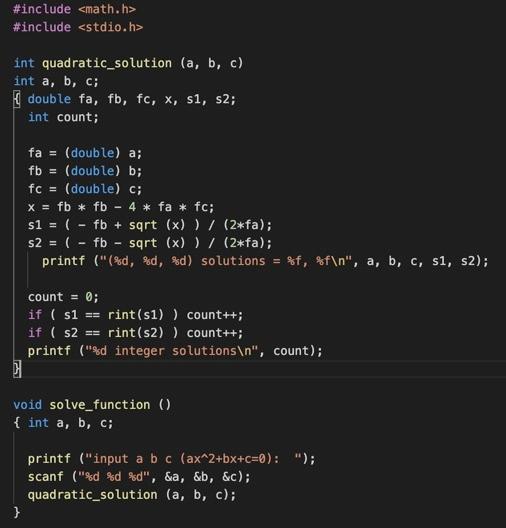
#include main() { int cmd; do { printf ("command> "); scanf ("%d", &cmd); if (cmd = 1) solve_function (); else if (cmd == 2) find_numbers (); else if (cmd !=0) printf ("Invalid command "); } while (cmd !=0); } #include #include int is_square (x, y) int x, y: { double tx, ty, tz, tr, r; tx = (double) x; ty (double) y; tz = tx * tx + ty * ty; tr = sqrt (tz); if ( tr rint(tr)) return ((int) tr); else return (0); } int relatively prime (x, y) int x, y; { int tmp, r; if (x #include int quadratic_solution (a, b, c) int a, b, c; double fa, fb, fc, x, s1, s2; int count; fa = (double) a; fb = (double) b; fc = (double) c; x = fb * fb - 4 * fa * fc; s1 = ( - fb + sqrt (x) ) / (2*fa); s2 = ( - fb - sart (x) ) / (2*fa); printf ("%d, %d, d) solutions = $f, %f ", a, b, c, s1, s2); count = 0; if ( si rint(sl) ) count++; if ( s2 rint(s) ) count++; printf ("%d integer solutions ", count); ) void solve_function() { int a, b, c; printf ("input a b c (ax^2+bx+c=0): "); scanf ("%d %d %d", &a, &b, &c); quadratic_solution (a, b, c); } #include main() { int cmd; do { printf ("command> "); scanf ("%d", &cmd); if (cmd = 1) solve_function (); else if (cmd == 2) find_numbers (); else if (cmd !=0) printf ("Invalid command "); } while (cmd !=0); } #include #include int is_square (x, y) int x, y: { double tx, ty, tz, tr, r; tx = (double) x; ty (double) y; tz = tx * tx + ty * ty; tr = sqrt (tz); if ( tr rint(tr)) return ((int) tr); else return (0); } int relatively prime (x, y) int x, y; { int tmp, r; if (x #include int quadratic_solution (a, b, c) int a, b, c; double fa, fb, fc, x, s1, s2; int count; fa = (double) a; fb = (double) b; fc = (double) c; x = fb * fb - 4 * fa * fc; s1 = ( - fb + sqrt (x) ) / (2*fa); s2 = ( - fb - sart (x) ) / (2*fa); printf ("%d, %d, d) solutions = $f, %f ", a, b, c, s1, s2); count = 0; if ( si rint(sl) ) count++; if ( s2 rint(s) ) count++; printf ("%d integer solutions ", count); ) void solve_function() { int a, b, c; printf ("input a b c (ax^2+bx+c=0): "); scanf ("%d %d %d", &a, &b, &c); quadratic_solution (a, b, c); }