Unit2ProblemsSet(Summer 2024)

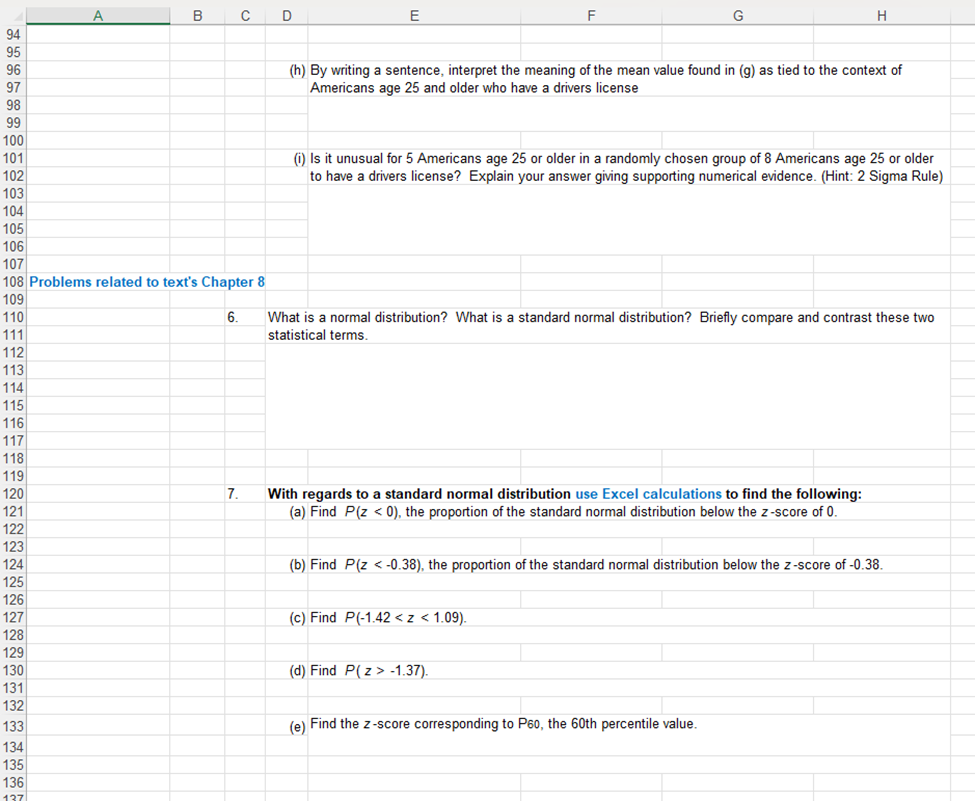
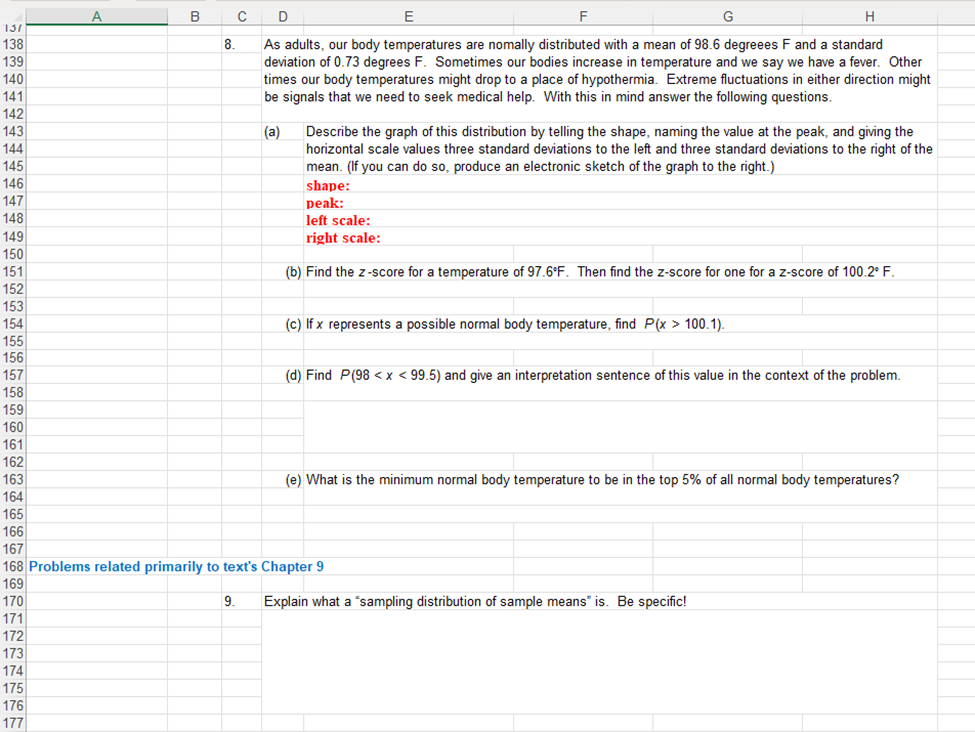
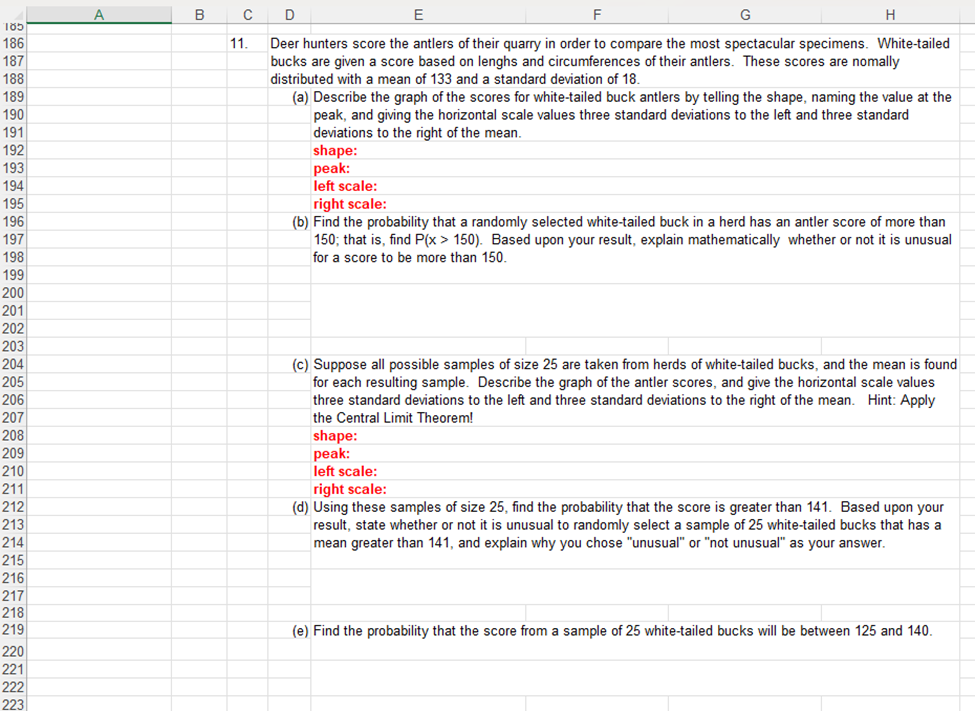
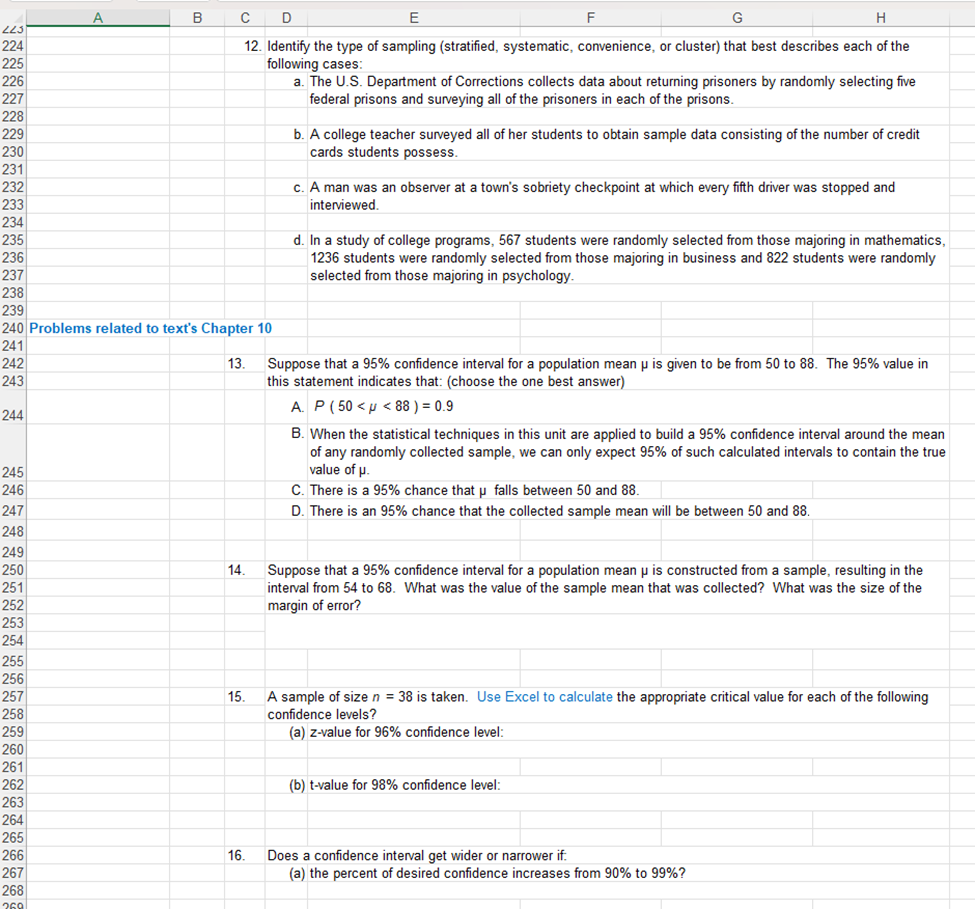
A B C D E F G H I J K L 5 & REMEMBER, these are assessed preparatory problems related to the content of Unit 2, The Unit 2 Exam will consist of similar types of problems, but not exactly the same. 7 Thus, make sure you are thinking about the concepts and procedures you studied in this unit versus simply \"copying\" the process of an example problem. Also, take time to 8 examine the complate objective list in the Unit 2 Topical Review document. Listed out to the left of the spreadsheet are text chapter separators if you find yourself needing 9 some direction to a related resource. All answers should be calculated, as needed, to the right of a problem within this Excel sheet, and final concluding answers given directly 10 below or to the night of the problem. Please make your answers easily found-for example use a different color or type of font. No numerical answer resulting from a 1 calculation will be accepted unless the process is performed in Excel and formulas/calculations used are evident when the cell is selected. 12 13 Type your name at the top, complete and return this file saved as \"youmame Unit2ProblemsSet\" through the Exam Prep region in Blackboard (from the same location that you 14 downloaded this file ) This problems set is due no later than July 5, 2024, Your instructor will grade and retum it to you with feedback to assist you in preparing for the Unit 2 15 Exam. 16 17 Problems related to text's Chapter 7 18 19 1. Identify each of the random vanables described below as discrete or continuous 20 a. The number of cartons of ice cream sold at Wal-Mart in Hays today. 21 22 23 b. The amount of time it takes to play a football game. 24 25 26 c. The number of pitches the starting pitcher for the Royals pitches in a game. 27 28 29 2. The incomplete probability distribution table at the right is of the discrete random vaniable x representing the 30 number of colds a person gets in one year. Answer the following: X P{X=x 3 (a) Determine the value that is missing in the table. (Hint: what are the requirments. for a probabilty destributon?) 0 0.05 32 1 011 33 2 0.18 k71 (b) Find the probability that x is at most 4, that is find P{x -1.37). 131 132| 133| (e) Find the z-score corresponding to P&o, the 60th percentile value. 134 135| 136| 4127 A B C D E F G H 131 138 8. As adults, our body temperatures are nomally distributed with a mean of 98.6 degreees F and a standard 139 deviation of 0.73 degrees F. Sometimes our bodies increase in temperature and we say we have a fever. Other 140 times our body temperatures might drop to a place of hypothermia. Extreme fluctuations in either direction might 141 be signals that we need to seek medical help. With this in mind answer the following questions. 142 143 (a) Describe the graph of this distnbution by telling the shape, naming the value at the peak, and giving the 144 horizontal scale values three standard deviations to the left and three standard deviations to the right of the 145 mean. (If you can do so, produce an electronic sketch of the graph to the right.) 146 shape: 147 peak: 148 left scale: 149 right scale: 150 151 (b) Find the z-score for a temperature of 97.6F. Then find the z-score for one for a z-score of 100.2* F. 152 153 154 (c) If x represents a possible normal body temperature, find P(x > 100.1). 155 156 157 (d) Find P(98 150). Based upon your result, explain mathematically whether or not it is unusual for a score to be more than 150. (c) Suppose all possible samples of size 25 are taken from herds of white-tailed bucks, and the mean is found for each resulting sample. Describe the graph of the antler scores, and give the horizontal scale values three standard deviations to the left and three standard deviations to the right of the mean. Hint: Apply the Central Limit Theorem! shape: peak: left scale: right scale: (d) Using these samples of size 25, find the probability that the score is greater than 141. Based upon your result, state whether or not it is unusual to randomly select a sample of 25 white-tailed bucks that has a mean greater than 141, and explain why you chose "unusual\" or "not unusual\" as your answer. (e) Find the probability that the score from a sample of 25 white-tailed bucks will be between 125 and 140. 43] 224 225/ 226 227 228| 229 230 23 232 233| 234| 235 236 237 238 239 240 241 242| ClRlD N i F | G _ H 12. Identify the type of sampling (stratified, systematic, convenience, or cluster) that best describes each of the following cases: a. The U.S. Department of Corrections collects data about returning prisoners by randomly selecting five federal prisons and surveying all of the prisoners in each of the prisons. b. A college teacher surveyed all of her students to obtain sample data consisting of the number of credit cards students possess. c. A man was an observer at a town's sobriety checkpoint at which every fifth driver was stopped and interviewed. d. In a study of college programs, 567 students were randomly selected from those majoring in mathematics, 1236 students were randomly selected from those majoring in business and 822 students were randomly selected from those majoring in psychology. jProbiems related to text's Chapter 10 243 244| 245 246/ 247| 248)| 249 250| 251 252 253 254 255 257| 253 259 260/ 261 262| 263 264 265 266 267| 268| 280 13 14. 15. 16. Suppose that a 95% confidence interval for a population mean p is given to be from 50 to 88. The 95% value in this statement indicates that: (choose the one best answer) A P(50