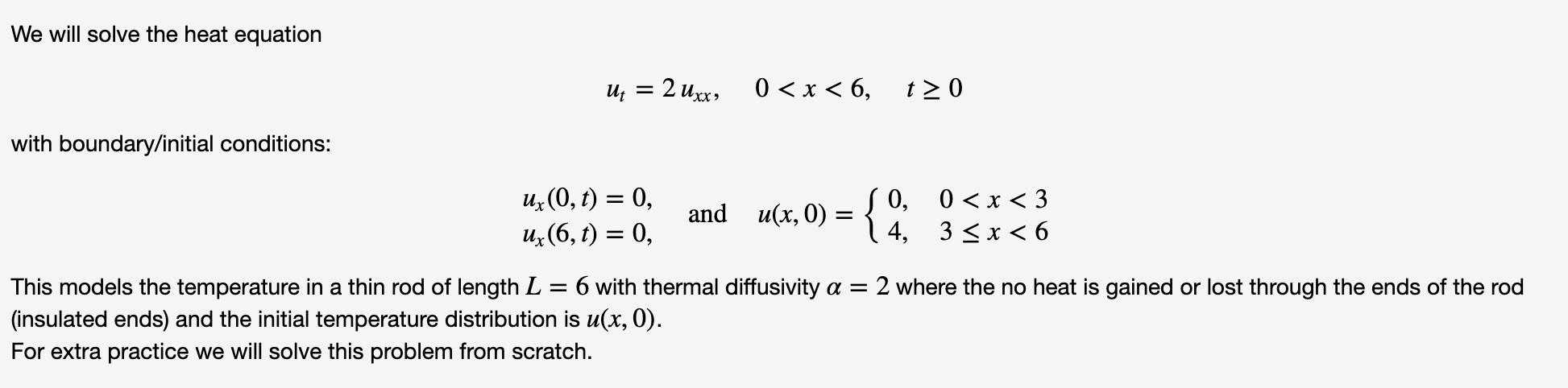
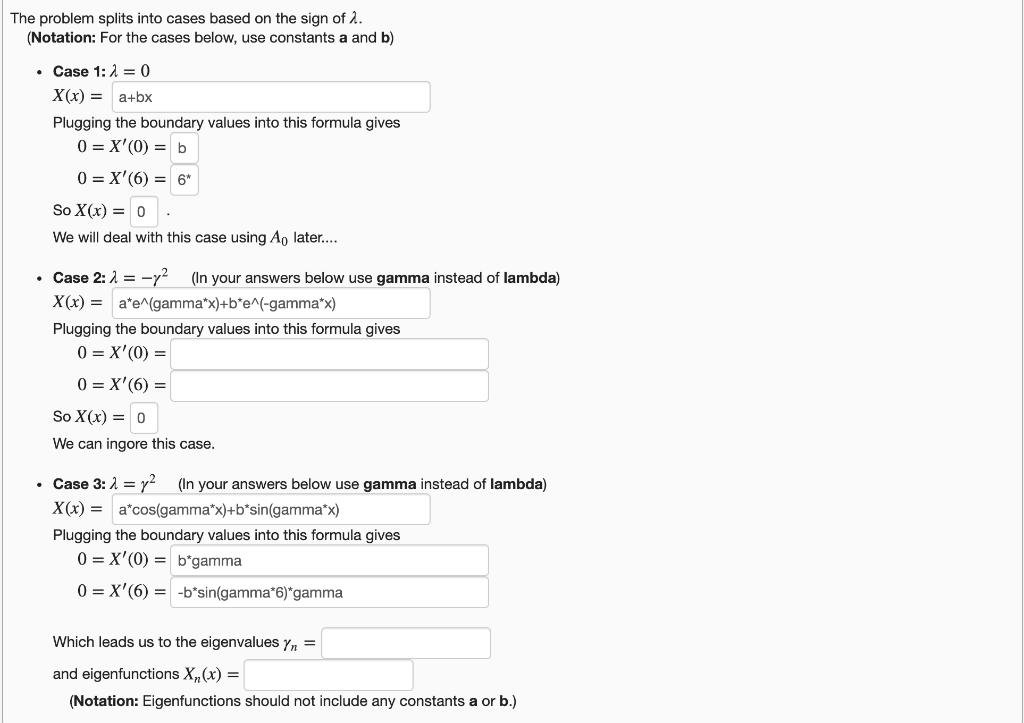
We will solve the heat equation with boundary/initial conditions: Ut = 2 Uxx, ux (0, t) = 0, ux (6, t) = 0, 0 < x < 6, t> 0 0 The problem splits into cases based on the sign of 2. (Notation: For the cases below, use constants a and b) Case 1:1=0 X(x) = a+bx Plugging the boundary values into this formula gives 0 = X'(0) = b 0=X'(6) = 6* So X(x) = 0 We will deal with this case using Ao later.... Case 2: = -y (In your answers below use gamma instead of lambda) X(x) = a*e^(gamma*x)+b*e^(-gamma*x) Plugging the boundary values into this formula gives 0 = X'(0) = 0 = X'(6) = So X(x) = 0 We can ingore this case. Case 3: = y (In your answers below use gamma instead of lambda) X(x) = a*cos(gamma*x)+b*sin(gamma*x) Plugging the boundary values into this formula gives 0=X'(0) = b*gamma 0 X'(6)= -b*sin(gamma*6)*gamma Which leads us to the eigenvalues Y = and eigenfunctions X, (x) = (Notation: Eigenfunctions should not include any constants a or b.) Plug the eigenvalues Any from Case 3 into the differential equation for T(t) and solve: Tn (t) = (Notation: use c for the unknown constant.) Combining all of the X and Tn we get that u(x, t) = An n=0 where A, are unknown constants.