Let \(\left\{X_{n}ight\}\) be a sequence of random variables having binomial densities, where \(X_{n}\) has a binomial density with parameters \(n\) and \(p\), i.e.,

\(X_{n} \sim\left(\begin{array}{c}n \\ x\end{array}ight) p^{x}(1-p)^{n-x} I_{\{0,1,2, \ldots n\}}(x)\).

(a) Show that \(\left(X_{n}-n pight) /\left(\sqrt{n}(p(1-p))^{1 / 2}ight) \xrightarrow{\text { d }} N(0,1)\).

(b) Define an asymptotic distribution for \(X_{n}\). Use Van Beeck's inequality to provide a bound on the error in approximating the probability \(P\left(x_{n} \leq cight)\) using the asymptotic distribution for \(X_{n}\). Calculate the numerical value of this bound when \(p=.3\).

(c) Using the binomial density for \(X_{n}\), and letting \(p=.3\), it follows that

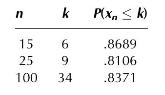
Assign (approximate) probabilities to the three events using asymptotic distributions based on your answer for (b). How good are the approximations?

(d) In using the CLT to approximate probabilities of events for discrete random variables whose range consists of equally spaced points, it has been found that a continuity correction improves the accuracy of the approximation. In particular, letting \(R(X)=\left\{x_{1}, x_{2}, x_{3}, \ldotsight\}\) where \(x_{i+1}-x_{i}=2 h>0 \forall i\), the continuity correction involves treating each elementary event \(x_{j}\) for the discrete random variable \(X\) as the interval event \(\left(x_{j}-h, x_{j}+hight]\) for the normal asymptotic distribution of the random variable \(X\). For example, if \(R(X)=\{0,1,2,3, \ldots\}\) then \(P(x \in[1,2])=\sum_{x=1}^{2} f(x) \approx \hat{P}(x \in(.5,2.5])\), where the latter (approximate) probability is assigned using the appropriate asymptotic normal distribution for \(X\). Use the continuity correction to approximate the probabilities of the three events in (c).

Transcribed Image Text:

n k 15 6 25 9 100 34 P(xnk) .8689 .8106 .8371