Testing for Differences in Two Populations: Means (Unequal Variances) (The Behrens-Fisher Problem).

Consider the hypotheses in Problem (3) in the case where it is not assumed that the variances of the two populations are equal.

(a) Attempt to find a GLR test of the hypothesis \(H_{0}\) : \(\mu_{1}=\mu_{2}\) versus \(H_{a}\) : not \(H_{0}\) based on a t-statistic similar to what you found in (3) above. Is this approach valid? The problem of testing hypotheses concerning the means of two normal population distributions when it is not assumed that the variances are equal is known as the Behrens-Fisher problem, which as of yet has no universally accepted solution.

One reasonable solution to this problem is to use the statistic

\(t=\frac{\bar{x}_{1}-\bar{x}_{2}}{\left(s_{1}^{2} / n_{1}+s_{2}^{2} / n_{2}ight)^{1 / 2}}\)

where \(n_{1}\) and \(n_{2}\) refer to the respective sample sizes of samples from the two populations. It can be shown that a test of size \(\leq \alpha\) of any of the hypotheses concerning the means of the two population distributions given in (3a)-(3c) can be performed by defining rejection regions as follows:

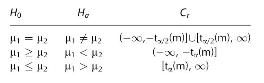The value of \(t_{\alpha}(m)\) is a typical critical value of the student \(t\) distribution found in \(t\)-tables, except the degrees of freedom parameter \(m=\min \left(n_{1}, n_{2}ight)\). The procedure is sometimes referred to as the Hsu procedure. Further discussion of the Behrens Fisher problem can be found in H. Scheffe, (1970), "Practical Solutions of the Behrens-Fisher Problems," JASA, 65, pp. 1501-1508.

(b) Using the Hsu procedure discussed above, test the hypothesis of the equality of the means in the population distributions referred to in Problems (1) and (2) above.

Transcribed Image Text:

Ho 11 (-, -t(m)] [t(m), x)