7.6 We have stressed that the wavefunction of a quantum mechanical particle does not directly represent the trajectory of that particle through space. This is very unlike the way in which we typically formulate classical mechanics, in which Newton's laws, for example, directly quantify the response of a particle's trajectory to external forces. Additionally, classical mechanics exhibits a "smoothness" in which particle trajectories are continuous and differentiable functions in space and time. In this problem, we will study properties of quantum mechanical trajectories and attempt to determine ways in which they are similar or different to that of classical trajectories. This problem has been analyzed in the literature, \({ }^{5}\) and here we will explore some aspects of that paper's conclusions.
The central quantity we will use to study the trajectory of a quantum mechanical particle is its dimension. We define it in the following way. Imagine dividing up the trajectory in steps of size \(\Delta x\). Then, the sum of all such steps is the total length \(\ell\) of the trajectory. In general, note that \(\ell\) depends on the resolution length \(\Delta x\). However, we can introduce a length that is independent of \(\Delta x\), which we call the Hausdorff length \(L\) :

\[\begin{equation*}L=\lim _{\Delta x \rightarrow 0} \ell(\Delta x)^{D-1} \tag{7.130}\end{equation*}\]
where \(D\) is a quantity chosen so that \(L\) is independent of resolution \(\Delta x\). The quantity \(D\) is called the Hausdorff dimension of the curve, \({ }^{6}\) and if \(D eq 1\), the curve is a fractal: continuous but everywhere non-smooth. \({ }^{7}\) Classical particle trajectories have Hausdorff dimension \(D=1\); that is, they are smooth curves. What is the dimension of a quantum mechanical trajectory?
5 L. F. Abbott and M. B. Wise, "The dimension of a quantum mechanical path," Am. J. Phys. 49, 37-39 (1981).
6 F. Hausdorff, "Dimension und äußeres Maß," Math. Ann. 79, 157-179 (1918).
7 B. B. Mandelbrot, "How long is the coast of Britain? Statistical self-similarity and fractional dimension," Science 156(3775), 636-638 (1967).

(a) We have just stated that smooth curves have Hausdorff dimension \(D=1\). Argue that this must be the case.
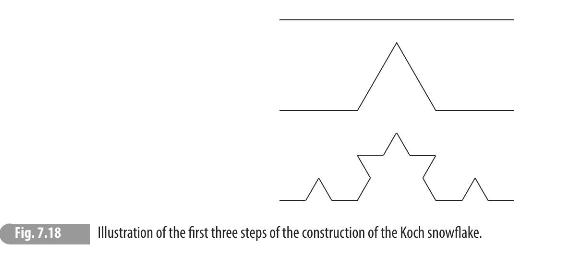
(b) A classical example of a continuous but everywhere non-smooth curve is the Koch snowflake. \({ }^{8}\) It can be iteratively constructed and the first few steps of the construction are shown in Fig. 7.18. The procedure continues ad infinitum, with each straight segment replaced by four segments in a kinked shape, with each segment being one-third the length of the segment at the previous step. From the definition provided above, determine the Hausdorff dimension for the Koch snowflake.
(c) With this warm-up, let's determine the Hausdorff dimension of the trajectory of a quantum mechanical particle of mass \(m\). We will assume that the average momentum of the particle is \(0,\langle\hat{p}angle=0\). Using the Heisenberg uncertainty principle, determine a relationship between the step size \(\Delta x\) and a time step \(\Delta t\). Assume that the Heisenberg uncertainty is saturated. Now, if the total elapsed time of the trajectory is \(T=N \Delta t\), what is its length \(\ell\) ? Then, what is the Hausdorff dimension?
(d) Let's relax the assumption that the average momentum is 0 . Let's assume that \(\langle\hat{p}angle=p_{0}\) and, from the steps in part (c), what is the Hausdorff dimension of the trajectory of such a quantum mechanical particle now? Does the \(p_{0} \rightarrow \infty\) limit match with your expectation from the correspondence principle?

Given \(\langle\hat{p}angle\), can you determine \(\left\langle\hat{p}^{2}\rightangle\) in terms of the variance of momentum?
(e) Now redo parts (c) and (d) from the perspective of the one-dimensional free particle wavefunction, instead of the Heisenberg uncertainty principle. See the Abbott and Wise paper for hints.

Transcribed Image Text:

Fig. 7.18 Illustration of the first three steps of the construction of the Koch snowflake.