Suppose that the sales manager of a large automotive parts distributor wants to estimate as early as April the total annual sales of a region. On the basis of regional sales, the total sales for the company can also be estimated. If, based on past experience, it is found that the April estimates of annual sales are reasonably accurate, then in future years the April forecast could be used to revise production schedules and maintain the correct inventory at the retail outlets. Several factors appear to be related to sales, including the number of retail outlets in the region stocking the company’s parts, the number of automobiles in the region registered as of April 1, and the total personal income for the first quarter of the year. Five independent variables were finally selected as being the most important (according to the sales manager). Then the data were gathered for a recent year. The total annual sales for that year for each region were also recorded. Note in the following table that for region 1 there were 1,739 retail outlets stocking the company’s automotive parts, there were 9,270,000 registered automobiles in the region as of April 1, and so on. The sales for that year were $37,702,000.

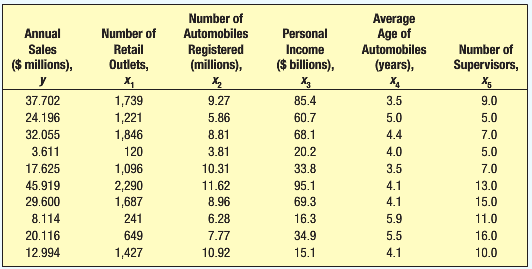
a. Consider the following correlation matrix. Which single variable has the strongest correlation with the dependent variable? The correlations between the independent variables outlets and income and between cars and outlets are fairly strong. Could this be a problem? What is this condition called?

b. The output for all five variables is shown below. What percent of the variation is explained by the regression equation?

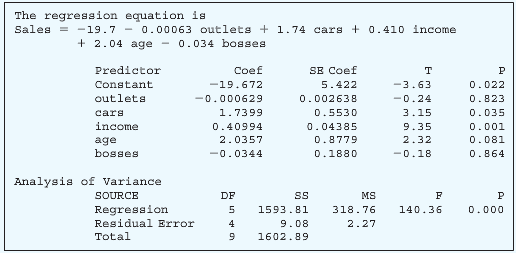
c. Conduct a global test of hypothesis to determine whether any of the regression coefficients are not zero. Use the .05 significance level.

d. Conduct a test of hypothesis on each of the independent variables. Would you consider eliminating “outlets” and “bosses”? Use the .05 significance level.

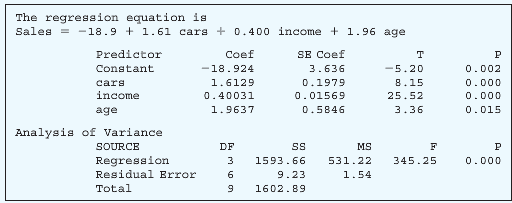
e. The regression has been rerun below with “outlets” and “bosses” eliminated. Compute the coefficient of determination. How much has R² changed from the previous analysis?

f. Following is a histogram of the residuals. Does the normality assumption appear reasonable?

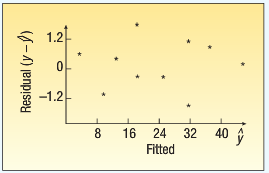
g. Following is a plot of the fitted values of y (i.e., yˆ) and the residuals. Do you see any violations of the assumptions?

Transcribed Image Text:

Average Age of Automobiles Number of Automobiles Annual Number of Personal Registered (millions), Sales Retail Income Number of ($ millions), Outlets, ($ billions), х, (years), Supervisors, х, 9.27 85.4 3.5 37.702 1,739 9.0 1,221 24.196 5.86 60.7 5.0 5.0 32.055 1,846 8.81 68.1 4.4 7.0 3,81 20.2 3.611 120 4.0 5.0 17.625 1,096 10.31 33.8 3.5 7.0 45.919 2,290 1,687 11.62 95.1 4.1 13.0 29.600 8.96 69.3 4.1 15.0 8.114 241 6.28 16.3 5.9 11.0 20.116 649 7.77 34.9 5.5 16.0 1,427 12.994 10.92 15.1 4.1 10.0