The A & M convenience store in Rock Mont, Illinois, has kept track of customer arrivals during the early morning hours of 1 a.m. to 4 a.m., collecting a sample of 300 hours of data. Below is a table showing the results of the study:

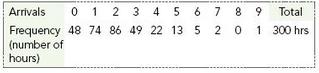
Conduct an appropriate chi square goodness of fit test to test a null hypothesis that the hourly arrival rate for A & M customers during the early morning hours has a Poisson distribution. Use the mean hourly arrival rate for the sample data as your estimate of the mean, of the Poisson distribution that you will try to “fit “to the sample data. Use a 5% level of significance. To meet the minimum expected frequency cell size requirement, you can combine arrival categories 6, 7, 8, and 9 into a single “6 or more arrivals “category. Compute degrees of freedom as c–2, where c is the number of categories after combining 6 through 9. (The reason that df is not computed as c–1 as described in the chapter is that one additional degree of freedom is lost when the sample mean is used to estimate the population mean.)

Transcribed Image Text:

Arrivals 0 2 3 4 5 6 7 89 Total Frequency 48 74 86 49 22 13 5 2 0 1 300 hrs (number of hours)