The data for this exercise were taken from a chemical assay of calcium discussed in Brown, Healy, and Kearns (1981). A set of standard solutions is prepared, and these and the unknowns are read on a spectrophotometer in arbitrary units (y). A linear regression model is fit to the standards, and the values of the unknowns (x) are read off from this. The preparation of the standard and un-known solutions involves a fair amount of laboratory manipulation, and the actual concentrations of the standards may differ slightly from their target values, the very precise instrumentation being capable of detecting this. The target values are 2.0, 2.0, 2.5, 3.0, 3.0 mmol per liter; the '' duplicates'' are made up independently. The sequence of reading the standards and unknowns is repeated four times. Two specimens of each unknown are included in each assay, and the four sequences of readings are done twice, first with the flame conditions in the instrument optimized and then with a slightly weaker flame. y is the spectrophotometer reading and x is the actual mmol per liter.
The data in the following table relate to assays on the above pattern of a set of six unknowns performed by four laboratories. The standards are identified as 2.0A, 2.0B, 2.5, 3.0A, and 3.0B; the unknowns are identified as U1, U2, W1, W2, Y1, and Y2.

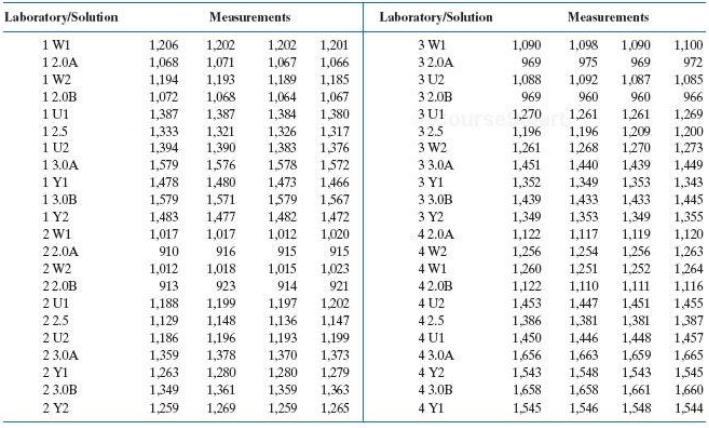
a. Plot y versus x for the standards, one graph for each laboratory.
b. Fit the linear regression equation y = β0 + β1x + ɛ for each laboratory, and predict the value of x corresponding to the y for each of the unknowns. Compute the standard deviation of the predicted values of x based on the four predicted x- values for each of the unknowns.
c. Which laboratory appears to make better predictions of x, mmol of calcium per liter? Why?

Transcribed Image Text:

Laboratory/Solution Measurements Laboratory/Sohution Measurements 1 W1 1,206 1,068 1,194 1,202 1,071 1,193 1,068 1,202 1,201 3 W1 1,090 1,098 1,090 1,100 12.0A 1,067 1,066 32.0A 969 975 969 972 1 W2 3 U2 32.0B 3U1 1,189 1,085 1,185 1,067 1,088 1,092 1,087 12.0B 1 U1 125 1 U2 13.0A 1 Y1 1,072 1,064 969 960 960 966 1,387 1,333 1,394 1,384 1.326 1,383 1,270 1,196 1,261 1,387 1,380 1,261 1,261 1,269 1209 1,270 1,200 1,273 325 1.321 1,390 1,317 1,196 1,268 1,376 3 W2 1576 1,480 1,571 1,477 1,579 3 3.0A 3 YI 1,451 1,352 1,439 1,578 1,572 1,440 1,439 1,449 1.478 1,473 1.466 1,349 1,353 1,343 1,579 1,483 33.0В 1,433 1,353 13.0B 1,579 1,482 1,567 1,433 1,445 1 Y2 1,472 1,020 3 Y2 1,349 1,349 1,355 2 W1 1,017 1,017 1,012 42.0A 1,122 1,117 1,119 1,120 1,263 4 W2 4 W1 1,256 1.254 1,251 22.0A 910 916 915 915 1,256 2 W2 1,012 1,015 1,252 1,023 921 1,018 1,260 1264 1,122 1,453 22.0B 913 923 914 42.0B 1,110 1,111 1,116 1,202 1,147 4 U2 42.5 2 U1 1,188 1,447 1,199 1,148 1,197 1,451 1,455 1,129 1,186 1,359 1,263 22.5 1,136 1386 1,381 1,381 1,387 4 U1 43.0A 2 U2 1,196 1,193 1,199 1,450 1,446 1,448 1,457 2 3.0A 1,378 1,370 1,373 1,656 1,663 1,659 1,665 2 YI 1,280 1,280 1.279 4 Y2 1,543 1,548 1543 1,545 2 3.0B 1,349 1,361 1,359 1,363 4 3.0B 1,658 1,658 1,661 1,660 2 Y2 1,259 1,269 1,259 1,265 4 YI 1,545 1,546 1,548 1,544