The data in the table below were collected in a famous social psychological field experiment. The researchers examined a common source of frustration for drivers: a car stopped at a traffic light that fails to move when the light turns green. The variable they manipulated was the status of the frustrating car (1 = high status, expensive, new; 0 = low status, inexpensive, old). They ran repeated trials in which they stopped at a red light, waited for the light to turn green – and then did not move the car; they observed whether the driver in the car behind them honked or not (honked = 1, did not honk = 0). They predicted that people would be more likely to honk at low status cars than high status cars (Doob, A. N., & Gross, A. E. (1968), Status of frustrator as an inhibitor of horn-honking responses. Journal of Social Psychology, 76, 213-218.

This table reports part of their results:

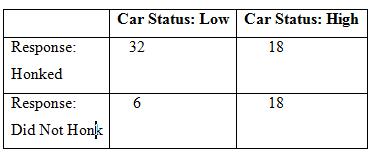
a. Calculate ϕ and χ² by hand for the table above, and write up a Results section that describes your findings and notes whether the researcher’s prediction was upheld.

b. Enter the data for this table into SPSS. To do this, create one variable that contains scores of 0 or 1 for the variable “status” and another column for the variable that contains the scores of 0 or 1 for the variable “honking”. (For example, because there were 18 people who honked at a high status car, you will enter 18 lines with scores of 1, 1.)

c. Using SPSS, do the following: run the Cross tabs procedure and obtain both ϕ and χ²; also, run a bivariate correlation (and note how the obtained bivariate correlation compares to your obtained ϕ).

d. In this situation, given the marginal frequencies, what is the maximum possible value of ϕ?

e. The researchers manipulated the independent variable (status of car) and were careful to control for extraneous variables. Can they make a causal inference from these results? Why or why not?

Transcribed Image Text:

Car Status: Low Car Status: High 18 Response 32 Honked Response Did Not Honk 18