The information about in a random sample of size n is also given by Where f

The information about θ in a random sample of size n is also given by

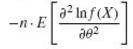
Where f (x) is the value of the population density at x, provided that the extremes of the region for which f(x) ≠ 0 do not depend on θ. The derivation of this formula takes the following steps: 

(a) Differentiating the expressions on both sides of 

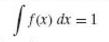
With respect to θ, show that

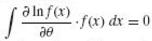
By interchanging the order of integration and differentiation. 

(b) Differentiating again with respect to θ, show that

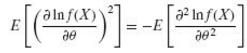
Transcribed Image Text:

a2 Inf(X) ge2 f(x) dx = 1 a Inf(x)-f(x) dx = 0 a2 InfX) alnfx)2 ge