Use the result of part (b) of Exercise 5.14 to show that for the binomial distribution Where

Question:

Use the result of part (b) of Exercise 5.14 to show that for the binomial distribution

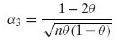
Where α₃ is the measure of skewness defined in Exercise 4.26 on page 129. What can we conclude about the skewness of the binomial distribution when

(a) θ = 1/2;

(b) n is large?

Distribution
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...