With reference to Definition 4.4, show that 0 = 1 and that 1 = 0

Question:

With reference to Definition 4.4, show that µ₀ = 1 and that µ₁ = 0 for any random variable for which E(X) exists.

Definition 4.4

The rth moment about the mean of a random variable X, denoted by µ_r, is the expected value of ( X – µ)^r, symbolically

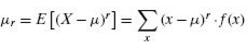
For r = 0, 1, 2, . . . , when X is discrete, and

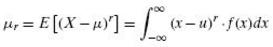
When X is continuous.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:05 AM

See More Questions

Show that if 1 < 0 in Example 12.4, the Neyman-Pearson lemma yields the critical region IS po - Za
With reference to the generalized definition of binomial coefficients in Exercise 1.19, show that (a) (b) -l r) = (1)r (n+r-1 for n>0
With reference to Exercise 5.12, find the factorial momentgenerating function of (a) The Bernoulli distribution and show that µ'(1) = . and µ'(r) = 0 for r > 1; (b) The binomial...
A manufacturer of packaging for companies that produce breakfast cereals is considering alternatives regarding the process it uses to pre-process carton paper used to make the packaging....
Use Table 2 in Appendix B to determine the critical region used in testing each of the following hypotheses. a. Ho: p = 0.5 and Ha: p > 0.5 where n = 15 and a = 0.05 b. Ho: p = 0.5 and Ha: p 0.3...
If a force of F = 50 N acts on the rope, determine the cutting force on the smooth tree limb at D and the horizontal and vertical components of force acting on pin A. The rope passes through a small...
Show that the pure shrinkage estimator (Problem 9.25) is the solution to Data From Problem 9.25 The pure shrinkage estimator is defined as $\hat{\beta}_{s}=c \hat{\beta}$, were $0 \leq c \leq 1$...
Willard Company manufactures three different sizes of automobile sunscreens: large, medium, and small. Willard expects to incur $360,000 of overhead costs during the next fiscal year. Other budget...
relations are true for every n1: a) i=1 1 n (21-1)(2i+1) 2n+1 b) 13-1 = (3n-1) Using mathematical induction, show that the following
You are given the following Gibbs free energy: aT5/2 G = -kBTNln P Where kg is the Boltzmann constant, N is the number of atoms, a is a constant whose units make the argument of the logarithm...
If the probability distribution of X is given by f(x) = (1/2)x for x = 1, 2, 3, . . . show that E(2X) does not exist. This is the famous Petersburg paradox, according to which a players expectation...
Find , '2, and s2 for the random variable X that has the probability distribution f(x) = 12 for x = 2 and x = 2.
Find the points on the surface y 2 = 9 + xz that are closest to the origin.
Are there any actions Tatum could take to achieve both her professional goals and worklife balance?
Are there any other obstacles that Guava may encounter when transitioning employees to remote work? How could the company limit the number of obstacles?
Provide two examples of personal expenses that are deductible on an individuals tax return.
Which of these includes the benefits of teamwork? Organizational enhancement Self-development and growth Helps in providing mutual support All of the above
How does motivation and intention play a role, for both you and your coworker
Jager Metal Corp. Equity Section of the Balance Sheet November 30, 2023 Contributed capital: Required Refer to the equity section above. Assume that the preferred shares are convertible into common...
Use a calculator to evaluate the expression. Round your result to the nearest thousandth. V (32 + #)
The Georgetown, South Carolina, Traffic Division reported 40% of high-speed chases involving automobiles result in a minor or major accident. During a month in which 50 high-speed chases occur, what...
Cruise ships of the Royal Viking line report that 80% of their rooms are occupied during September. For a cruise ship having 800 rooms, what is the probability that 665 or more are occupied in...
The goal at U.S. airports handling international flights is to clear these flights within 45 minutes. Lets interpret this to mean that 95% of the flights are cleared in 45 minutes, so 5% of the...
Frank is 82 years old.His wife died 5 years ago.He died and left the following assets: Principal residence 859,000 (individually owned: ACB 350,000) RRIF $235,000 (Beneficiary adult daughter ACB...
Assume that Pope Enterprises held a $10,000, 10 percent, six-month note signed by Mary Drew. On December, 1, 2015, the maturity date, Drew dishonored the note. At this point, Drew owes a total of...
5. Consider the shape shown on the following graph and the brute force method of solving the convex hull problem 2 -2 -1 0 a. Label all the points that will be provided to the algorithm as input. You...

With reference to Definition 4.4, show that 0 = 1 and that 1 = 0

Question:

4, = E[(X-uY] = Ea-u f)

Step by Step Answer:

H fx fx d...View the full answer

John E Freunds Mathematical Statistics With Applications

Students also viewed these Statistics questions