Question: With reference to Example 10.3, we showed on page 281 that X 1 is an unbiased estimator of d, and in Exercise 10.8 the

With reference to Example 10.3, we showed on page 281 that X̅ – 1 is an unbiased estimator of d, and in Exercise 10.8 the reader was asked to find another unbiased estimator of d based on the smallest sample value. Find the efficiency of the first of these two estimators relative to the second.

Example 10.3

If X₁, X₂, . . . , X_n constitute a random sample from the population given by

[e-(x-5) for x > elsewhere

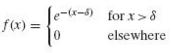
Show that X̅ is a biased estimator of ∂.

[e-(x-5) for x > elsewhere

Step by Step Solution

★★★★★

3.36 Rating (168 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Yx1 ZY1n EY nye nf u 8 enu du 0 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

583-M-S-P-E (780).docx

120 KBs Word File

Students Have Also Explored These Related Statistics Questions!

Large-Sample Test of a 2 = ? 0 2 : When n > 30 we can test the null hypothesis that ? = ? 0 2 , or ? ? (To, by computing which is a value of a random variable whose sampling distribution is...

With reference to Example 10.3, find an unbiased estimator of d based on the smallest sample value (that is, on the first order statistic, Y 1 ). Example 10.3 If X 1 , X 2 , . . . , X n constitute a...

With reference to Example 10.4, find an unbiased estimator of based on the smallest sample value (that is, on the first order statistic, Y1). Example 10.4 If X1, X2, . . . , Xn constitute a random...

9/14/10 12:27 PM Page 321 Chapter dug84356_ch05a.qxd 5 Factoring The sport of skydiving was born in the 1930s soon after the military began using parachutes as a means of deploying troops. Today,...

Set Student Name: 1. Answer true or false for each part, and if false, explain your answer. a. The point estimate for the population mean, , of an x distribution is x-bar, computed from a random...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

Rev.Confirming Pages C H A P T E R 7 Planning, Composing, and Revising Chapter Outline The Ways Good Writers Write Activities in the Composing Process Using Your Time Effectively Brainstorming,...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Graham purchased a business by agreeing to make three payments of $12 000 each in one year, two years, and four years. Because of cash flow difficulties in the first year, he renegotiated the payment...

Successful Mining Company (SMC) specializes in extracting ore. It prides itself for following high environmental standards in the extraction process. On January 1, 2022, SMC purchased the rights to...

11.64 Suppose that you were given a 95% confidence interval for the relative risk of disease under two different conditions. What could you conclude about the comparison of the risk of disease under...

Let us say you work as consultant after graduating from university. Learning from the mistakes of LG.Philips Displays and LG.PhilipsLCD joint venture activities, what would you recommended to make an...

In a murder trial in Los Angeles, the prosecution claims that the defendant was cut on the left middle finger at the murder scene, but the defendant claims the cut occurred in Chicago, the day after...

Suppose that A 1 , A2 , and B are events where A1 and A2 are mutually exclusive and P(A1 ) =.8 P( B A1 )= .1 P( A2 ) =.2 P( B A2 )= .3 Use this information to find P (A1 B) and P (A2 B).

Suppose that A1, A2 , A3 , and B are events where A1 , A2 , and A3 are mutually exclusive and P (A1) =.2 P (A2) =.5 P (A3) = .3 P (B A1) = .02 P (B A2) =.05 P( B A3 )=.04 Use this information to find...

What is the one - year rate of return on a $ 1 , 0 0 0 face value bond with a coupon rate of 5 % that had a price of $ 9 4 9 at the beginning of the year and $ 1 , 1 0 4 at the end of the year? (...

Dennis wants to determine if the discount rate really makes any difference in the net present value of a project. He feels that if a project is acceptable at one rate of return, it will be acceptable...

i have the answer , just need a detailed explanation how they got it. If a person earns $3,000 per month and 25% can be used for PITI; What is the maximum price house that person can afford if the...