With reference to Exercise 4.8, find the variance of g(X) = 2X + 3. In exercise for
Question:
With reference to Exercise 4.8, find the variance of g(X) = 2X + 3.
In exercise
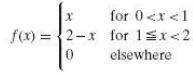
Transcribed Image Text:
for 0
for 0
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 64% (17 reviews)
var 2x 3 4 varx 1 from ...View the full answer

Answered By

Junaid ahmed
I am an English language professor with years of experience In Teaching English Language and Literature. I like to help people in the various difficult matter.
5.00+
2+ Reviews
10+ Question Solved
Related Book For 

John E Freunds Mathematical Statistics With Applications
ISBN: 9780134995373
8th Edition
Authors: Irwin Miller, Marylees Miller
Question Posted:
Students also viewed these Statistics questions
-
With reference to Exercise 3.47 on page 90, find E(2X Y).
-
With reference to Exercise 3.74 on page 100, find cov( X, Y).
-
With reference to Exercise 4.71, what can we assert about the amount of time it takes a person to be served at the given restaurant if we use Chebyshevs theorem with k = 1.5? What is the...
-
1. (Adverse Selection) Consider a labor market model with many identical firms hiring workers. The firms produce a homogeneous product with a constant-returns-to-scale technology and act as price...
-
For each of the following pairs of values, state the decision that will occur and why. a. p-value = 0.018, a = 0.01 b. p-value = 0.033, a = 0.05 c. p-value = 0.078, a = 0.05 d. p-value = 0.235, a =...
-
Determine the reactions at the fixed support E and the smooth support A. The pin, attached to member BD, passes through a smooth slot atD. 600 N 0.4 m 0,4 m -0.3 m- -0.3 m- -0.3 m- 0.3 m-
-
Estimate model parameters for the Hald cement data (Table B.21) using principal-component regression. a. What is the loss in \(R^{2}\) for this model compared to least squares?b. How much shrinkage...
-
Brokia Electronics manufactures three cell phone models, which differ only in the components included: Basic, Photo, and UrLife. Production takes place in two departments, Assembly and Special...
-
4. Istanbul Municipality wants to know if a Flood Control Project is economically feasible. Annual Benefits $1,200,000; Annual Disbenefits $ 200,000; Initial Cost of the Project= $3,000,000 Annual...
-
The following merchandise transactions occurred in December. Both companies use a perpetual inventory system. Dec. 3 Swifty Ltd. sold goods to Blue Spruce Corp. for $ 73,500 terms 2/10, n/30, FOB...
-
Prove Theorem 4.7. Theorem 4.7 If X has the variance 2, Then var(aX + b) = a22
-
If the random variable X has the mean and the standard deviation s, show that the random variable Z whose values are related to those of X by means of the equation z = x- / has E(Z) = 0 and var(Z)...
-
On November 23, 2013, Radon Mines Company acquired new machinery by trading in old machinery and paying $23,000 cash plus another $15,000 borrowed from the bank at 8%. The new machinery's estimated...
-
Evaluate the following statement: Policies to redistribute income are desperately needed in the United States. Without such policies, the roughly 13 percent of the population that is currently poor...
-
Imagine that you are appointed as a leader of a project and you are preparing for the first meeting, identify important actions you could take to have a positive influence on the team members.
-
Let X X be a drifted Brownian motion with positive drift and y y its last passage time at level y y . Prove that P x ( ( ) y d t ) = 2 t exp ( 1 2 t ( x y + t ) 2 ) d t P x ( y ( ) ...
-
What do you think would be the ideal decision in this situation and why? Does the ideal decision differ from what your coworker proposes?
-
Firoz, a 28-year-old woman, works in a mental hospital as a technician for the last three years. In the beginning, she found the job interesting and value added. As time passed, the environment began...
-
Multiply or divide as indicated. w - 16 W 3 4-w W
-
For a nonzero constant a, find the intercepts of the graph of (x 2 + y 2 ) 2 = a 2 (x 2 - y 2 ). Then test for symmetry with respect to the x-axis, the y-axis, and the origin.
-
Refer to the Baseball 2012 data, which report information on the 30 Major League Baseball teams for the 2012 season. a. The mean attendance per team for the season was 2.495 million, with a standard...
-
Refer to the Buena School District bus data. a. Refer to the maintenance cost variable. The mean maintenance cost for last year is $450.29, with a standard deviation of $53.69. Estimate the number of...
-
Explain what is meant by this statement: There is not just one normal probability distribution but a family of them.
-
For each ordered pair, determine -6x+7y=2 7x-4y=6 a solution to the system of equations.
-
Review the meaning of the concepts or terms given in Key Terms and Concepts. Distinguish between a production department and a service department. Distinguish between a direct cost and an indirect...
-
What would you like the members of your learning community to know about your global health interests, perspectives, and life experiences? How will you prepare to listen and learn from others? Why...

Study smarter with the SolutionInn App


