Creeping flow between two concentric spheres (Fig. 3B.4). A very viscous Newtonian fluid flows in the space
Question:
Creeping flow between two concentric spheres (Fig. 3B.4). A very viscous Newtonian fluid flows in the space between two concentric spheres, as shown in the figure. It is desired to find the rate of flow in the system as a function of the imposed pressure difference. Neglect end effects and postulate that vθ depends only on r and θ with the other velocity components zero.
(a) Using the equation of continuity, show that vθ sin θ = u(r), where u(r) is a function of r to be determined.
(b) Write the θ-component of the equation of motion for this system, assuming the flow to be slow enough that the [v ∙ ∆v] term is negligible. Show that this gives
(c) Separate this into two equations where B is the separation constant, and solve the two equations to get where P1 and P2 are the values of the modified pressure at θ = ε and θ = π – ε, respectively.
(d) Use the results above to get the mass rate of flow
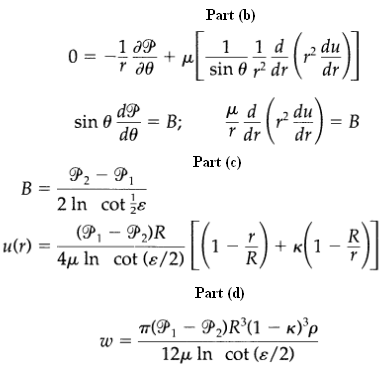
Step by Step Answer:






