Show that for a finite group, a subnormal series with solvable quotient groups can be refined to a composition series with abelian quotients, thus completing the proof of Theorem 56.4.

Data from Theorem 56.4

Let F be a field of characteristic zero, and let F ≤ E ≤ K ≤ F̅, where E is a normal extension of F and K is an extension of F by radicals. Then G(E/F) is a solvable group.

Proof We first show that K is contained in a finite normal extension L of F by radicals and that
the group G(L/F) is solvable. Since K is an extension by radicals, K = F(α₁,· · ·,α_r)  where α_iⁿⁱ ∈ F(α₁,· · ·, α_i-1) for 1 < i ≤nr and a¹ , a-1) for 1 < i 1ⁿ¹ ∈ F. To form L, we first form the splitting field L₁ of f₁(x) = xⁿ¹ -  α₁ⁿ¹ over F. Then L₁ is a normal extension of F, and Lemma 56.3 shows that G(L₁/F) is a solvable group. Now α₂ⁿ² ∈ L₁ and we form the polynomial

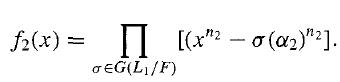
Since this polynomial is invariant under action by any σ in G(L₁/F), we see that
f₂(x) ∈ F[x]. We let L₂ be the splitting field of f₂(x) over L₁. Then L₂ is a splitting field over F also and is a normal extension of F by radicals. We can form L₂ from L₁ via repeated steps as in Lemma 56.3, passing to a splitting field of xⁿ² - σ(α₂)ⁿ² at each step. By Lemma 56.3 and Exercise 7, we see that the Galois group over F of each new extension thus formed continues to be solvable. We continue this process of forming splitting fields over F in this manner: At stage i, we form the splitting field of the polynomial

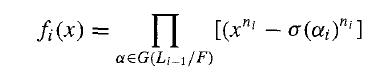
over L_i-1. We finally obtain a field L = L_r that is a normal extension of F by radicals, and we see that G(L/F) is a solvable group. We see from construction that K ≤ L. To conclude, we need only note that by Theorem 53.6, we have G(E/F) ≈ G(L/F)/ G(L/E). Thus G(E/F) is a factor group, and hence a homomorphic image, of G(L/F). Since G(L/F) is solvable, Exercise 29 of Section 35 shows that G(E/F) is solvable.

Transcribed Image Text:

f₂(x) = П [(x¹¹² - σ (α₂)¹¹²]. σEG(L₁/F)