This exercise exhibits a polynomial of degree 5 in Q[x] that is not solvable by radicals over Q.

a. Show that if a subgroup H of S₅ contains a cycle of length 5 and a transposition τ, then H = S₅.

b. Show that if f(x) is an irreducible polynomial in Q[x] of degree 5 having exactly two complex and three real zeros in C, then the group of f(x) over Q is isomorphic to S₅.

c. The polynomial f(x) = 2x⁵ - 5x⁴ + 5 is irreducible in Q[x], by the Eisenstein criterion, with p = 5. Use the techniques of calculus to find relative maxima and minima and to "graph the polynomial function f" well enough to see that f(x) must have exactly three real zeros in C. Conclude from part (b) and Theorem 56.4 that f(x) is not solvable by radicals over Q.

Data from Theorem 56.4

Let F be a field of characteristic zero, and let F ≤ E ≤ K ≤ F̅, where E is a normal extension of F and K is an extension of F by radicals. Then G(E/F) is a solvable group.

Proof We first show that K is contained in a finite normal extension L of F by radicals and that the group G(L/F) is solvable. Since K is an extension by radicals, K = F(α₁,· · ·,α_r) where α_iⁿⁱ ∈ F(α₁,· · ·, α_i-1) for 1 < i ≤nr and a¹ , a-1) for 1 < i 1ⁿ¹ ∈ F. To form L, we first form the splitting field L₁ of f₁(x) = xⁿ¹ - α₁ⁿ¹ over F. Then L₁ is a normal extension of F, and Lemma 56.3 shows that G(L₁/F) is a solvable group. Now α₂ⁿ² ∈ L₁ and we form the polynomial

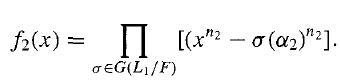
Since this polynomial is invariant under action by any σ in G(L₁/F), we see that f₂(x) ∈ F[x]. We let L₂ be the splitting field of f₂(x) over L₁. Then L₂ is a splitting field over F also and is a normal extension of F by radicals. We can form L₂ from L₁ via repeated steps as in Lemma 56.3, passing to a splitting field of xⁿ² - σ(α₂)ⁿ² at each step. By Lemma 56.3 and Exercise 7, we see that the Galois group over F of each new extension thus formed continues to be solvable. We continue this process of forming splitting fields over F in this manner: At stage i, we form the splitting field of the polynomial

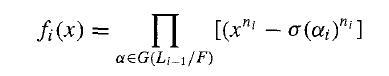
over L_i-1. We finally obtain a field L = L_r that is a normal extension of F by radicals, and we see that G(L/F) is a solvable group. We see from construction that K ≤ L. To conclude, we need only note that by Theorem 53.6, we have G(E/F) ≈ G(L/F)/ G(L/E). Thus G(E/F) is a factor group, and hence a homomorphic image, of G(L/F). Since G(L/F) is solvable, Exercise 29 of Section 35 shows that G(E/F) is solvable.

Transcribed Image Text:

f(x) = Π [(x2 – σ(α2)^2]. σεG(L/F)