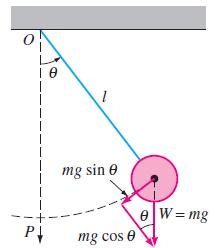
For the simple pendulum described on page 220 of Section 5.3, suppose that the rod holding the mass m at one end is replaced by a flexible wire or string and that the wire is strung over a pulley at the point of support O in Figure 5.3.3. In this manner, while it is in motion in a vertical plane, the mass m can be raised or lowered. In other words, the length l(t) of the pendulum varies with time. Under the same assumptions leading to equation (6) in Section 5.3, it can be shown* that the differential equation for the displacement angle θ is now

lθ'' + 2l'θ' + g sin θ = 0.

(a) If l increases at constant rate v and if l (0) = l₀, show that a linearization of the foregoing DE is

(l₀ + vt)θ'' + 2vθ' + gθ = 0.

(b) Make the change of variables x = (l₀ + vt) v and show that (34) becomes

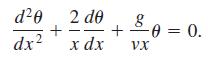
(c) Use part (b) and (18) to express the general solution of equation (34) in terms of Bessel functions.

(d) Use the general solution obtained in part (c) to solve the initial-value problem consisting of equation (34) and the initial conditions θ(0) = θ₀, θ'(0) = 0.

To simplify calculations, use a further change of variable

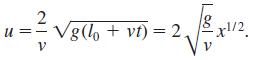
Also, recall that (20) holds for both J₁(u) and Y₁(u). Finally, the identity

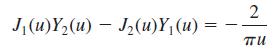
will be helpful.

(e) Use a CAS to graph the solution θ(t) of the IVP in part (d) when l₀ = 1 ft, θ₀ = 1/10 radian, and v = 1/60 ft/s. Experiment with the graph using different time intervals such as [0, 10], [0, 30], and so on. (f) What do the graphs indicate about the displacement angle θ(t) as the length l of the wire increases with time?

Figure 5.3.3

Transcribed Image Text:

d20 2 de + x dx 8e = 0. .2 dx? VX