(a) Distance, Eccentricity. Call the length of a shortest path u †’ v in a graph G = (V, E) the distance d(u, v) from u to v. For fixed u, call the greatest d(u, v) as v ranges over V the eccentricity ϵ(u) of u. Find the eccentricity of vertices 1, 2, 3 in the graph in Prob. 7.

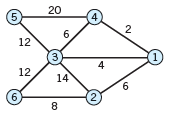
(b) The diameter d(G) of a graph G = (V, E) is the maximum of d(u, v) as u and v vary over V, and the radius r(G) is the smallest eccentricity ϵ(v) of the vertices v. A vertex v with ϵ(v) = r(G) is called a central vertex. The set of all central vertices is called the center of G. Find d(G), r(G), and the center of the graph in Prob. 7.

(c) What are the diameter, radius, and center of the spanning tree in Example 1 of the text?

(d) Show that a tree T whose edges all have length 1 has center consisting of either one vertex or two adjacent vertices.

(e) Set up an algorithm of complexity O(n) for finding the center of a tree T.

Data from Prob. 7

Transcribed Image Text:

20 5. 2 6. 12 (1 4 12 14 9. 6) 8.