We can gain more insight into Little’s law by considering Figure 2.8a. Over a period of time T, a total of C items arrive at a system, wait for service, and complete service. The upper solid line shows the time sequence of arrivals, and the lower solid line shows the time sequence of departures. The shaded area bounded by the two lines represents the total “work” done by the system in units of job-seconds; let A be the total work. We wish to derive the relationship among L, W, and λ.

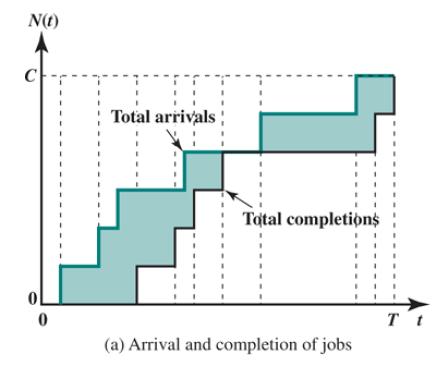
Figure 2.8a

a. Figure 2.8b divides the total area into horizontal rectangles, each with a height of one job. Picture sliding all these rectangles to the left so that their left edges line up at t = 0. Develop an equation that relates A, C, and W.

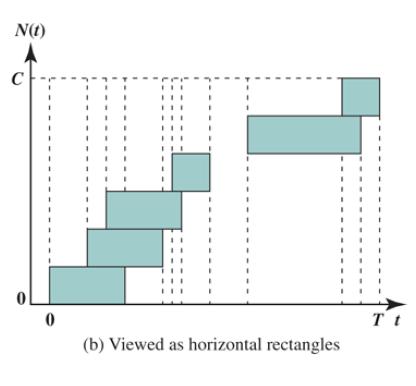
Figure 2.8b

b. Figure 2.8c divides the total area into vertical rectangles, defined by the vertical transition boundaries indicated by the dashed lines. Picture sliding all these rectangles down so that their lower edges line up at N(t) = 0. Develop an equation that relates A, T, and L.

Figure 2.8c

c. Finally, derive L = λW from the results of (a) and (b).

Transcribed Image Text:

N(1) T t (b) Viewed as horizontal rectangles