An inverted pendulum mounted on a motor-driven cart was introduced in Problem 30 in Chapter 3. Its state-space model was linearized around a stationary point, x₀ = 0 (Prasad, 2012). At the stationary point, the pendulum point-mass, m, is in the upright position at t = 0, and the force applied to the cart, u0, is 0. Its model was then modified in Problem 55 in Chapter 6 to have two output variables: the pendulum angle relative to the y-axis, θ(t), and the horizontal position of the cart, x(t). MATLAB was then used to find its eigenvalues. Noting that only one pole (out of four) is located in the left half of the s-plane, we concluded that this unit requires stabilization. To accomplish stability and design an appropriate control system, do the following:

a. Draw a signal-flow diagram for that unit and use it to develop Simulink models for two feedback systems: one to control the cart position, x(t), and the other to control the pendulum angle, θ(t). Set the upper and lower saturation limits of the second integrator in the angle loop to 100 and -100, respectively, and those limits in the position loop to 10 and -10.

b. Use rate feedback with a gain of 12.5 to stabilize the pendulum angle control system. The forward path of each of these systems should include a PD (proportional-plus-derivative) controller that adjusts the force applied to the cart, u(t). These controllers³ may be configured with the following settings:⁴

P = 5, I = 0, and D = 5 for the cart position controller

P = 2, I = 0, and D = 10 for the pendulum angle controller

c. Utilizing scopes to capture the two output responses, use a unit-impulse⁵ as the reference input in the angle control loop and a unit step source (configured to start at t = 0 with a final value of 1) as the input for the cart position control loop.

d. If either of the responses has a steady state error, e(∞)> 2%, a peak time, TP> 1.2 seconds, or a percent overshoot, %OS>20.5%, suggest appropriate changes to its controller settings.

Data From Problem 30 in Chapter 3:

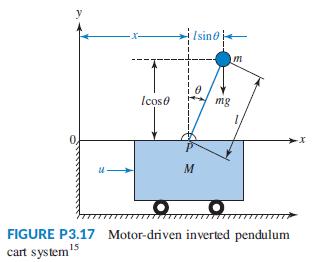
Figure P3.17 shows a free-body diagram of an inverted pendulum, mounted on a cart with a mass, M. The pendulum has a point mass, m, concentrated at the upper end of a rod with zero mass, a length, l, and a frictionless hinge. A motor drives the cart, applying a horizontal force, u(t). A gravity force, mg, acts on m at all times. The pendulum angle relative to the y-axis, θ, its angular speed, θ̇´, the horizontal position of the cart, x, and its speed, x´, were selected to be the state variables. The state-space equations derived were heavily nonlinear.¹⁴ They were then linearized around the stationary point, x₀ = 0 and u₀ = 0, and manipulated to yield the following open-loop model written in perturbation form: Figure P3.17 shows a free-body diagram of an inverted pendulum, mounted on a cart with a mass, M. The pendulum has a point mass, m, concentrated at the upper end of a rod with zero mass, a length, l, and a frictionless hinge. A motor drives the cart, applying a horizontal force, u(t). A gravity force, mg, acts on m at all times. The pendulum angle relative to the y-axis, θ, its angular speed, θ̇´ , the horizontal position of the cart, x, and its speed, x´, were selected to be the state variables. The state-space equations derived were heavily nonlinear.¹⁴ They were then linearized around the stationary point, x₀ = 0 and u₀ = 0, and manipulated to yield the following open loop model written in perturbation form:

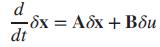
However, since x₀ = 0 and u₀ = 0, then let: x = x₀ + δx = δx and u = u₀ + δ_u = δu. Thus the state equation may be rewritten as (Prasad, 2012):

ẋ = Ax + Bu

where

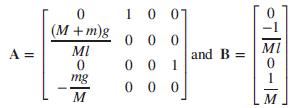
Assuming the output to be the horizontal position of m = x_m = x + l sinθ = x + lθ for a small angle, θ, the output equation becomes:

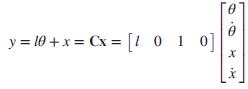
Given that: M = 2.4 kg, m = 0.23 kg, l = 0.36 m, g = 9.81 m/s², use MATLAB to find the transfer function, G(s)= Y(s)/U(s)= Xm(s)/U(s).

Transcribed Image Text:

d -Sx = Aôx + Bdu dt