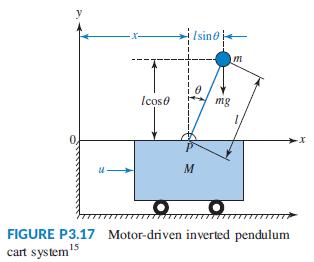
Figure P3.17 shows a free-body diagram of an inverted pendulum, mounted on a cart with a mass, M. The pendulum has a point mass, m, concentrated at the upper end of a rod with zero mass, a length, l, and a frictionless hinge. A motor drives the cart, applying a horizontal force, u(t). A gravity force, mg, acts on m at all times. The pendulum angle relative to the y-axis, θ, its angular speed, θ̇´, the horizontal position of the cart, x, and its speed, x´, were selected to be the state variables. The state-space equations derived were heavily nonlinear.¹⁴ They were then linearized around the stationary point, x₀ = 0 and u₀ = 0, and manipulated to yield the following open-loop model written in perturbation form: Figure P3.17 shows a free-body diagram of an inverted pendulum, mounted on a cart with a mass, M. The pendulum has a point mass, m, concentrated at the upper end of a rod with zero mass, a length, l, and a frictionless hinge. A motor drives the cart, applying a horizontal force, u(t). A gravity force, mg, acts on m at all times. The pendulum angle relative to the y-axis, θ, its angular speed, θ̇´ , the horizontal position of the cart, x, and its speed, x´, were selected to be the state variables. The state-space equations derived were heavily nonlinear.¹⁴ They were then linearized around the stationary point, x₀ = 0 and u₀ = 0, and manipulated to yield the following open loop model written in perturbation form:

However, since x₀ = 0 and u₀ = 0, then let: x = x₀ + δx = δx and u = u₀ + δ_u = δu. Thus the state equation may be rewritten as (Prasad, 2012):

ẋ = Ax + Bu

where

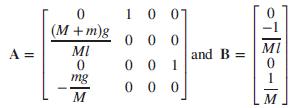
Assuming the output to be the horizontal position of m = x_m = x + l sinθ = x + lθ for a small angle, θ, the output equation becomes:

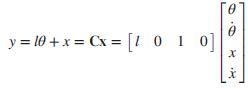
Given that: M = 2.4 kg, m = 0.23 kg, l = 0.36 m, g = 9.81 m/s², use MATLAB to find the transfer function, G(s)= Y(s)/U(s)= Xm(s)/U(s).

Transcribed Image Text:

d -Sx = Aôx + Bdu dt