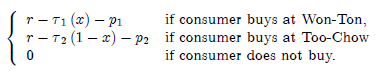Hong Kong Island features steep, hilly terrain, as well as hot and humid weather. Travelling up and down the slopes therefore causes problems; this has led the city authorities to imagine rather unusual methods of transport. One famous example can be found in the Western District, where one of the busiest commercial area of Hong Kong can be found. This area stretches from Des Voeux Road in Central (which is at sea level) up to Conduit Road in the Mid- Levels (which is the mid section of the hill of Hong Kong Island). Because the street is so steep, sidewalks are made of stairs. To make travelling up the slope easier for pedestrians, the Mid-Levels escalators  were opened to the public in October 1993. (Seehttp://www.12hk.com/area/Central/MidLevelEscalators.shtmlfor some pictures of the escalators and the stairs of this area). For the sake of this problem set, imagine the following story. Suppose that the street is one kilometre long (kilometre 0 is down at the crossroad with Des Voeux Road and kilometre one is up at the crossroad with Conduit Road). Suppose that 100,000 inhabitants are uniformly distributed along the street. Without loss of generality, we can approximate the consumer distribution by a continuum on [0, 1] with a mass set equal to 1 (i.e., we redefine all quantities by dividing them by 100,000). There are only two shops selling sweet-and-sour soup in this area. For simplicity, we set their marginal cost of production to zero. As it happens, one shop (named €˜Won €“ Ton€™ and indexed by 1) is located at point 0, while the other shop(named €™Too-Chow€™ and indexed by 2) is located at point 1. Everyday, each inhabitant of the street may consume at most one bowl of sweet-and-sour soup, bought either from Won-Ton or from Too-Chow. The price per bowl of the two shops are respectively denoted by p₁and p₂. The net utility for a consumer located at x o the interval [0, 1] is given by

where it is assumed that r is large enough so that every consumer buys one bowl of soup.

1. Before 1993 and the installation of the Mid-Levels escalators, walking up the street was much more painful than walking down. This is translated by the following assumptions: Ï„₁ (x) = tx and Ï„² (1 - x) = (t +Ï„) (1 - x), with t, Ï„ > 0.

(a) Derive the identity of the consumer who is indifferent between the two shops.

(b) Compute the equilibrium prices and profits of the two shops.

(c) Show that Two-Chow€™s profits increase if walking up the street be- comes more costly for consumers, that is if Ï„ increases (e.g., because the temperature has risen). Explain the intuition behind this result.

2. After 1993, the Mid-Levels escalators made going up and down equally painful for consumers. However, consumers had to pay a fixed fee f (independent of distance) to use the escalators. This is translated by the following assumptions: Ï„₁ (x) = tx and Ï„₂ (1 - x) = t (1 - x) + f, with f > 0.

(a) Derive the identity of the consumer who is indifferent between the two shops.

(b) Compute the equilibrium prices and profits of the two shops.

(c) Express the condition (in terms of f and t) under which the previous answers are valid (i.e. the condition for Too-Chow to set a price above its zero marginal cost).

(d) Show that Two-Chow€™s profits increase if taking the escalator becomes less expensive, that is if f decreases. Explain the intuition behind this result and contrast with your answer at (1c).

3. Comparing your answers for (1) and (2), establish and explain intuitively the following results.

(a) Too-Chow suffers from the installation of the escalators (even when its access is free, i.e., for f = 0).

(b) Won-Ton benefits from the installation of the escalators, unless the extra transportation cost of climbing the stairs (i.e., Ï„) is too large.

(To show this, set t = 2, f = 3 and compare Won-Ton€™s profits for Ï„ = 2 and Ï„ = 4).

Transcribed Image Text:

if consumer buys at Won-Ton, r - T2 (1 – x) – P2 if consumer buys at Too-Chow if consumer does not buy. r - T1 (x) – P