In Problem 11.1 you showed that the solution to

(where k(t) is a function of t) is

This suggests that the solution to the Schrödinger equation (11.1) might be

It doesn’t work, because Ĥ(t) is an operator, not a function, and Ĥ(t₁) does not (in general) commute with Ĥ(t₂).
(a) Try calculating iћ∂Ψ/∂t, using Equation 11.108.

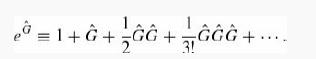
Show that if [Ĝ,Ĥ] = 0 then Ψ satisfies the Schrödinger equation

(b) Check that the correct solution in the general case ([Ĝ,Ĥ] ≠ 0) is

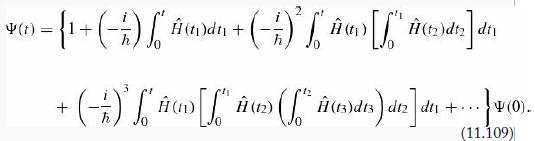
UGLY! Notice that the operators in each term are “time-ordered,” in the sense that the latest  Ĥ appears at the far left, followed by the next latest, and so on (t ≥ t₁ ≥ t₂ ≥ t₃ ...). Dyson introduced the time-ordered product of two operators:

or, more generally,

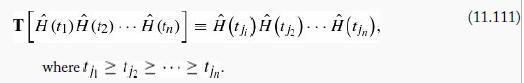
(c) Show that

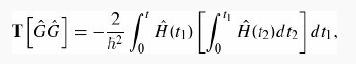
and generalize to higher powers of Ĝ. In place of Ĝⁿ, in equation 11.108, we really want T [Ĝⁿ]:

This is Dyson’s formula; it’s a compact way of writing Equation 11.109, the formal solution to Schrödinger’s equation. Dyson’s formula plays a fundamental role in quantum field theory.

Transcribed Image Text:

df dt =k(1) f(t)