In the photoelectric effect, light can ionize an atom if its energy () exceeds the binding energy

In the photoelectric effect, light can ionize an atom if its energy (ћω) exceeds the binding energy of the electron. Consider the photoelectric effect for the ground state of hydrogen, where the electron is kicked out with momentum ћk. The initial state of the electron is Ψ₀(r) (Equation 4.80) and its final state is

as in Example 11.2.
(a) For light polarized along the z direction, use Fermi’s Golden Rule to compute the rate at which electrons are ejected into the solid angle dΩ in the dipole approximation.

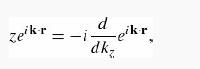
pull d/dk_z outside the integral, and what remains is straightforward to compute.
(b) The photoelectric cross section is defined as

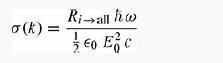
where the quantity in the numerator is the rate at which energy is absorbed ћω = ћ²k²/2m - E₁ per photoelectron) and the quantity in the denominator is the intensity of the incident light. Integrate your result from (a) over all angles to obtain R_i → all, and compute the photoelectric cross section.
(c) Obtain a numerical value for the photoelectric cross section for ultraviolet light of wavelength 220A (n.b. this is the wavelength of the incident light, not the scattered electron). Express your answer in mega-barns (Mb = 10^-22m²).

Transcribed Image Text:

Vf= 1 ik-r √13