Use the orthogonality properties of the spherical harmonics to prove the following identities for a function (r)

Use the orthogonality properties of the spherical harmonics to prove the following identities for a function φ(r) which satisfies Laplace’s equation in and on an origin-centered spherical surface S of radius R:

(a) ∫ dS φ(r) = 4πR²φ(0).

(b)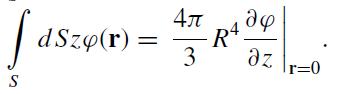

Transcribed Image Text:

I S dSzo(r) = = Ал 3 до R4 дz r=0