Crystals of Sodium Nitrate Na*(NO3) are trigonal with space group R-3c. When referred to a non...

Transcribed Image Text:

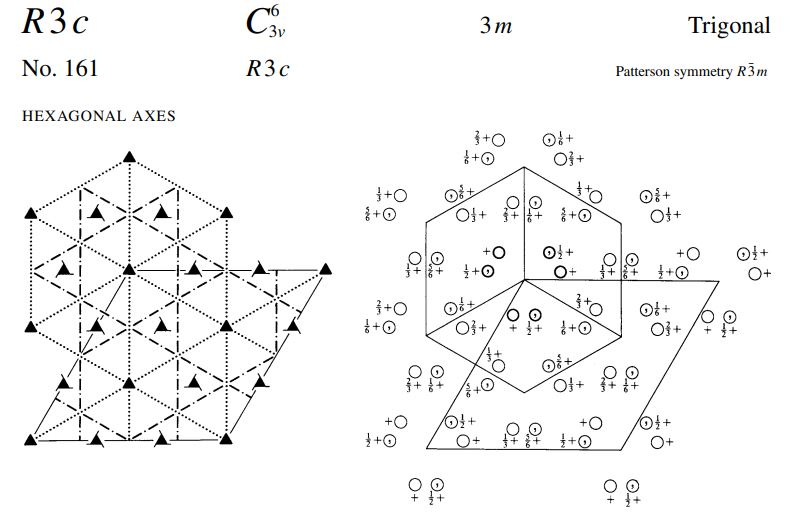
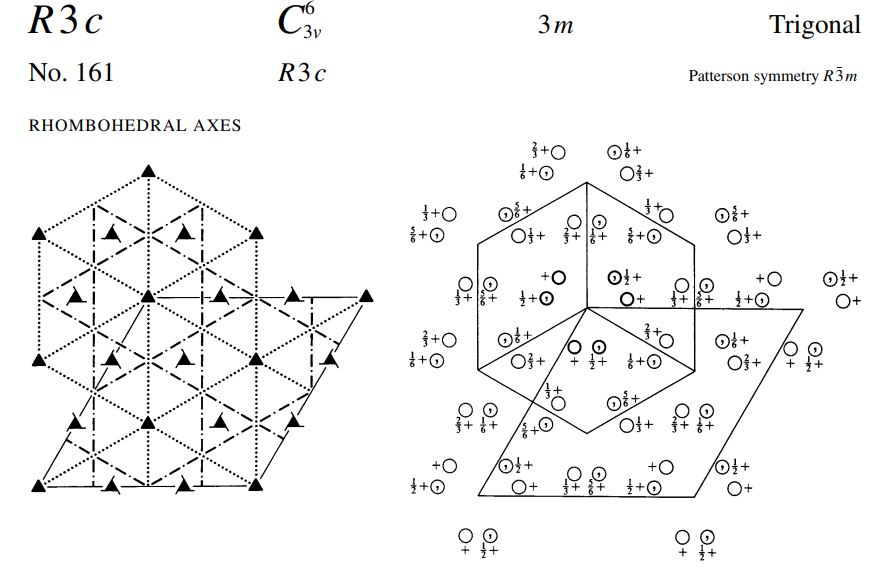
Crystals of Sodium Nitrate Na*(NO3) are trigonal with space group R-3c. When referred to a non primitive hexagonal lattice, the unit cell has a = 5.071 and c= 16.82. There are 6 (NaNO3) formula units in the cell. (Remember that NO3 is planar with the O's forming an equilateral triangle with the N in the middle) a) Use the International Tables to determine the crystal structure as completely as possible. b) What point symmetry is allowed for the NO, anion? c) What atomic positional parameters are not determined by the space group symmetry? R3c No. 161 HEXAGONAL AXES R3c O+f {+O O+ { O + f O+ O+F 3m 0+ { O+ Of+ 0}+ + ²/1/ + 10/ O+ +10 0+ +10 O+ O}+ Off +0 O+ toi 3+0 +O Of+ O+ O+f Patterson symmetry R3m Of+ Of+ O+F +10 Trigonal 0}+ Ⓒ++ O+ O+ Origin on 3 c Asymmetric unit Vertices 0≤x≤ 0≤y≤t: 0≤z≤ x ≤ (1+y)/2; y ≤min(1-x, (1+x)/2) 0,0,0,0,0,0.0 0,0,0,* * 0 Symmetry operations For (0,0,0) + set (1) 1 (4) c x,x,z For (+)+ set (1) *(4,4) (4) g() x+xz For (..)+ set (1) +(,,) (4) g() x+xz (2) 3+ 0,0,z (5) c x, 2x, z 0.4.0 (2) 3 (0,0,4) 4.4.2 (5) g() x+1,2x, z (2) 3 (0,0,4) 0,,z (5) g(..) x,2x, z (3) 3- 0,0,z (6) c 2x,x,z (3) 3 (0,0,1),0,z (6) g(,) 2x, x,z (3) 3 (0,0,1) 1.1.2 (6) g() 2x-1.x,z Positions Multiplicity. Wyckoff letter, Site symmetry 18 bl 6 a 3. 0,0,z Symmetry of special projections Along [001] p31m a = (2a+b) b = (-a+b) Origin at 0, 0, z (1) x,y,z (4) y,x,z++ IIa IIb none (0,0,0)+ (..)+ (..)+ [2] R31 (R3, 146) [3] R1c (Cc, 9) [3] RIc (Cc, 9) [3] R1c (Cc, 9) [3] P3c1 (158) Coordinates I II Maximal non-isomorphic subgroups I (1; 2; 3) + (1; 4)+ (1; 5)+ (1; 6)+ 1; 2; 3; 4; 5; 6 (2) y,x-y,z (5) x+y,y,z + + 0,0,z++ Minimal non-isomorphic supergroups (3) x+y, x, z (6) x,x-y,z++ Along [100] pl a' = (2a + 4b+c) Origin at x, 0,0 Maximal isomorphic subgroups of lowest index IIc [4] R3 c (a = -2a, b = -2b) (161); [5] R3c (a' = -a, b' = -b, c = 5c) (161) b=(-a-2b+c) Reflection conditions [2] R3c (167); [4] P43n (218); [4] F43c (219); [4] 143d (220) [2] R3 m (a = a, b = -b, c = c) (160); [3] P31c (a' = (2a+b), b = (-a+b), c = c) (159) General: hkil : -h+k+1=3n hki0 -h+k= 3n hh2hl: 1 = 3n hhol 0001 1= 6n hh00: h=3n Special: as above, plus hkil : 1 = 2n h+1=3n, 1 = 2n Along [210] plgl a = b b = c Origin at x, x,0 R3c No. 161 RHOMBOHEDRAL AXES 3v R3 c By +0 +O }+O +O +O +0 +O ++O O 3m 3+0 +O O+ Of+ +0 0}+ +0 Ot+ O+ Ⓒto +O 0}+ O+ +O Of+ + /O+ 00+ ++ + + +0 O+ Patterson symmetry R3m Of+ Of+ Ot+ Trigonal +0 +O 0}+ +O /Ⓒ++ O+ O+ 0+. Origin on 3 c Asymmetric unit Vertices 0≤x≤1; 0≤y≤1; 0≤z≤1; y≤x; z≤y 0,0,0 1,0,0 1,1,0 1,1,1 Symmetry operations (1) 1 (4) n() x,y,x Heights refer to hexagonal axes (2) 3 x, x,x (5) n() x,x, Z (3) 3 x, x,x (6) n() x,y,y Generators selected (1); t(1,0,0); t(0,1,0); t(0,0,1); (2); (4) Positions Multiplicity, Wyckoff letter, Site symmetry 6 b1 (1) x, y, z (4) z+y+x+ 2 a 3. X, X, X Symmetry of special projections Along [111] p31m a = (2a-b-c) b = (-a+2b-c) Origin at x, x,x Coordinates Maximal non-isomorphic subgroups I 1; 2; 3 1; 4 1; 5 1; 6 [2] R31 (R3, 146) [[3] R1c (Cc, 9) [3] R1c (Cc, 9) [[3] R1c (Cc, 9) I x+x+x+! II (2) z,x,y (5) y+x+z+! Ila none IIb [3] P3c1 (aa-b₁b-b-c,c=a+b+c) (158) Minimal non-isomorphic supergroups Along [110] pl a = + (a+b-2c) Origin at x.*,0 (3) y, z, x (6) x+z+y+ b = c Reflection conditions [2] R3c (167); [4] P43n (218); [4] F43c (219); [4] 143d (220) [2] R3m (a = (-a+b+c), b = (a-b+c), c = (a+b-c)) (160); [3] P31c (a=(2a-b-c), b=(-a+2b-c), c = (a+b+c)) (159) General: hhl: 1 = 2n hhh: h= 2n Maximal isomorphic subgroups of lowest index IIc [4] R3c (a' = -a+b+c,b=a-b+c,c=a+b-c) (161); [5] R3 c (a=a+2b+2c, b = 2a+b+2c, c = 2a+2b+c) (161) Special: as above, plus hkl h+k+1= 2n Along [211] p1g1 a = -(b-c) Origin at 2x, .*,* b = + (a+b+c) Crystals of Sodium Nitrate Na*(NO3) are trigonal with space group R-3c. When referred to a non primitive hexagonal lattice, the unit cell has a = 5.071 and c= 16.82. There are 6 (NaNO3) formula units in the cell. (Remember that NO3 is planar with the O's forming an equilateral triangle with the N in the middle) a) Use the International Tables to determine the crystal structure as completely as possible. b) What point symmetry is allowed for the NO, anion? c) What atomic positional parameters are not determined by the space group symmetry? R3c No. 161 HEXAGONAL AXES R3c O+f {+O O+ { O + f O+ O+F 3m 0+ { O+ Of+ 0}+ + ²/1/ + 10/ O+ +10 0+ +10 O+ O}+ Off +0 O+ toi 3+0 +O Of+ O+ O+f Patterson symmetry R3m Of+ Of+ O+F +10 Trigonal 0}+ Ⓒ++ O+ O+ Origin on 3 c Asymmetric unit Vertices 0≤x≤ 0≤y≤t: 0≤z≤ x ≤ (1+y)/2; y ≤min(1-x, (1+x)/2) 0,0,0,0,0,0.0 0,0,0,* * 0 Symmetry operations For (0,0,0) + set (1) 1 (4) c x,x,z For (+)+ set (1) *(4,4) (4) g() x+xz For (..)+ set (1) +(,,) (4) g() x+xz (2) 3+ 0,0,z (5) c x, 2x, z 0.4.0 (2) 3 (0,0,4) 4.4.2 (5) g() x+1,2x, z (2) 3 (0,0,4) 0,,z (5) g(..) x,2x, z (3) 3- 0,0,z (6) c 2x,x,z (3) 3 (0,0,1),0,z (6) g(,) 2x, x,z (3) 3 (0,0,1) 1.1.2 (6) g() 2x-1.x,z Positions Multiplicity. Wyckoff letter, Site symmetry 18 bl 6 a 3. 0,0,z Symmetry of special projections Along [001] p31m a = (2a+b) b = (-a+b) Origin at 0, 0, z (1) x,y,z (4) y,x,z++ IIa IIb none (0,0,0)+ (..)+ (..)+ [2] R31 (R3, 146) [3] R1c (Cc, 9) [3] RIc (Cc, 9) [3] R1c (Cc, 9) [3] P3c1 (158) Coordinates I II Maximal non-isomorphic subgroups I (1; 2; 3) + (1; 4)+ (1; 5)+ (1; 6)+ 1; 2; 3; 4; 5; 6 (2) y,x-y,z (5) x+y,y,z + + 0,0,z++ Minimal non-isomorphic supergroups (3) x+y, x, z (6) x,x-y,z++ Along [100] pl a' = (2a + 4b+c) Origin at x, 0,0 Maximal isomorphic subgroups of lowest index IIc [4] R3 c (a = -2a, b = -2b) (161); [5] R3c (a' = -a, b' = -b, c = 5c) (161) b=(-a-2b+c) Reflection conditions [2] R3c (167); [4] P43n (218); [4] F43c (219); [4] 143d (220) [2] R3 m (a = a, b = -b, c = c) (160); [3] P31c (a' = (2a+b), b = (-a+b), c = c) (159) General: hkil : -h+k+1=3n hki0 -h+k= 3n hh2hl: 1 = 3n hhol 0001 1= 6n hh00: h=3n Special: as above, plus hkil : 1 = 2n h+1=3n, 1 = 2n Along [210] plgl a = b b = c Origin at x, x,0 R3c No. 161 RHOMBOHEDRAL AXES 3v R3 c By +0 +O }+O +O +O +0 +O ++O O 3m 3+0 +O O+ Of+ +0 0}+ +0 Ot+ O+ Ⓒto +O 0}+ O+ +O Of+ + /O+ 00+ ++ + + +0 O+ Patterson symmetry R3m Of+ Of+ Ot+ Trigonal +0 +O 0}+ +O /Ⓒ++ O+ O+ 0+. Origin on 3 c Asymmetric unit Vertices 0≤x≤1; 0≤y≤1; 0≤z≤1; y≤x; z≤y 0,0,0 1,0,0 1,1,0 1,1,1 Symmetry operations (1) 1 (4) n() x,y,x Heights refer to hexagonal axes (2) 3 x, x,x (5) n() x,x, Z (3) 3 x, x,x (6) n() x,y,y Generators selected (1); t(1,0,0); t(0,1,0); t(0,0,1); (2); (4) Positions Multiplicity, Wyckoff letter, Site symmetry 6 b1 (1) x, y, z (4) z+y+x+ 2 a 3. X, X, X Symmetry of special projections Along [111] p31m a = (2a-b-c) b = (-a+2b-c) Origin at x, x,x Coordinates Maximal non-isomorphic subgroups I 1; 2; 3 1; 4 1; 5 1; 6 [2] R31 (R3, 146) [[3] R1c (Cc, 9) [3] R1c (Cc, 9) [[3] R1c (Cc, 9) I x+x+x+! II (2) z,x,y (5) y+x+z+! Ila none IIb [3] P3c1 (aa-b₁b-b-c,c=a+b+c) (158) Minimal non-isomorphic supergroups Along [110] pl a = + (a+b-2c) Origin at x.*,0 (3) y, z, x (6) x+z+y+ b = c Reflection conditions [2] R3c (167); [4] P43n (218); [4] F43c (219); [4] 143d (220) [2] R3m (a = (-a+b+c), b = (a-b+c), c = (a+b-c)) (160); [3] P31c (a=(2a-b-c), b=(-a+2b-c), c = (a+b+c)) (159) General: hhl: 1 = 2n hhh: h= 2n Maximal isomorphic subgroups of lowest index IIc [4] R3c (a' = -a+b+c,b=a-b+c,c=a+b-c) (161); [5] R3 c (a=a+2b+2c, b = 2a+b+2c, c = 2a+2b+c) (161) Special: as above, plus hkl h+k+1= 2n Along [211] p1g1 a = -(b-c) Origin at 2x, .*,* b = + (a+b+c)