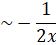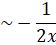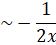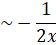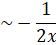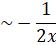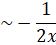Q1. Consider the Airy equation Show that, as x there are solutions Where are constants. Solution: Airy
Question:
Q1.
Consider the Airy equation
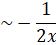
Show that, as x![]() there are solutions
there are solutions
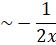
Where ![]() are constants.
are constants.
Solution:
Airy function Ai(x) is a special function and Bi(x) is linearly dependent solution to the differential equation
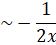
First we prove that

The asymptotes of Airy function is given by
Ai(x) = 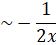
So, exp(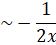
Now x![]()

Now, x![]() the solution will be
the solution will be
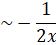
Where ![]() are constants.
are constants.
Q2.
Consider the nonlinear ODE

Confirm that 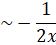 is an exact solution. Show that if there is another solution such that y(x)
is an exact solution. Show that if there is another solution such that y(x)![]() as
as 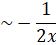 then
then
y(x)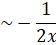 ,
,
where 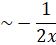 and C is a constant that cannot be determined from local analysis.
and C is a constant that cannot be determined from local analysis.
Solution:
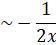
We now show that 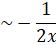 is an exact solution of the differential equation.
is an exact solution of the differential equation.
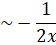 ,
, 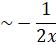
Again, (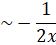
= (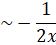
= ![]()
This shows that  is an exact solution of the differential equation.
is an exact solution of the differential equation.
Now let other solution of the differential equation be
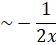
So, 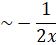
Let ![]()
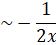
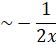
{
C ![]() F =
F = ![]()
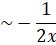
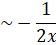
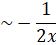
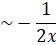
Therefore the another solution is
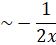
y(x) ,
, 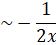
where 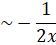 and C is a constant that cannot be determined from local analysis.
and C is a constant that cannot be determined from local analysis.
Q3.
Consider the behavior of solutions to the inhomogeneous Airy equation
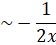
That decay as x![]() find the first two terms in the asymptotic expansion for y(x) as x
find the first two terms in the asymptotic expansion for y(x) as x![]() explain why the terms in the asymptotic power series are independent of an initial condition.
explain why the terms in the asymptotic power series are independent of an initial condition.
Solution:
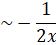 ………………………………………………………(i)
………………………………………………………(i)
Let us consider y = 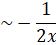
From (i)
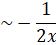
Now comparing both sides,
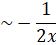
And
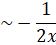
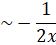
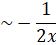 ,
, 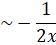 ,
, 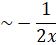
Again,
 ,
, 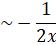 ,
, 
Again,
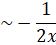
So, y(x) = 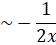
The first two terms are 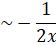 .
.
The terms in asymptotic power series is independent of initial conditions as it is a homogeneous Airy equation and there is one approximation like 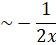 with non-zero terms
with non-zero terms 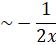
Q4.
Consider the equation
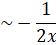
- Show that all three pair-wise dominant balances are inconsistent as
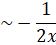
- Show that y(x)
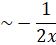 as
as  independent of an initial condition.
independent of an initial condition.
Solution:
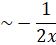
Let us consider the particular solution 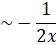
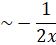

This is clearly not possible. This shows the pairwise dominant balances are inconsistent as ![]()
(b)
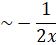 ………………………………………………..(i)
………………………………………………..(i)
Integrating factor of (i) = 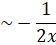 =
= ![]() =
= ![]()
Multiplying (i) by integrating factor and hence integrating, we have
y 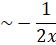 [where c is an integrating constant]
[where c is an integrating constant]
= 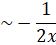
= 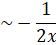
= 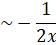
Now, 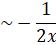
as ![]()
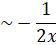
![]()
And it does not depend on the initial conditions.