Nine runners agree to participate in a study on two brands of shoes on the time...

 

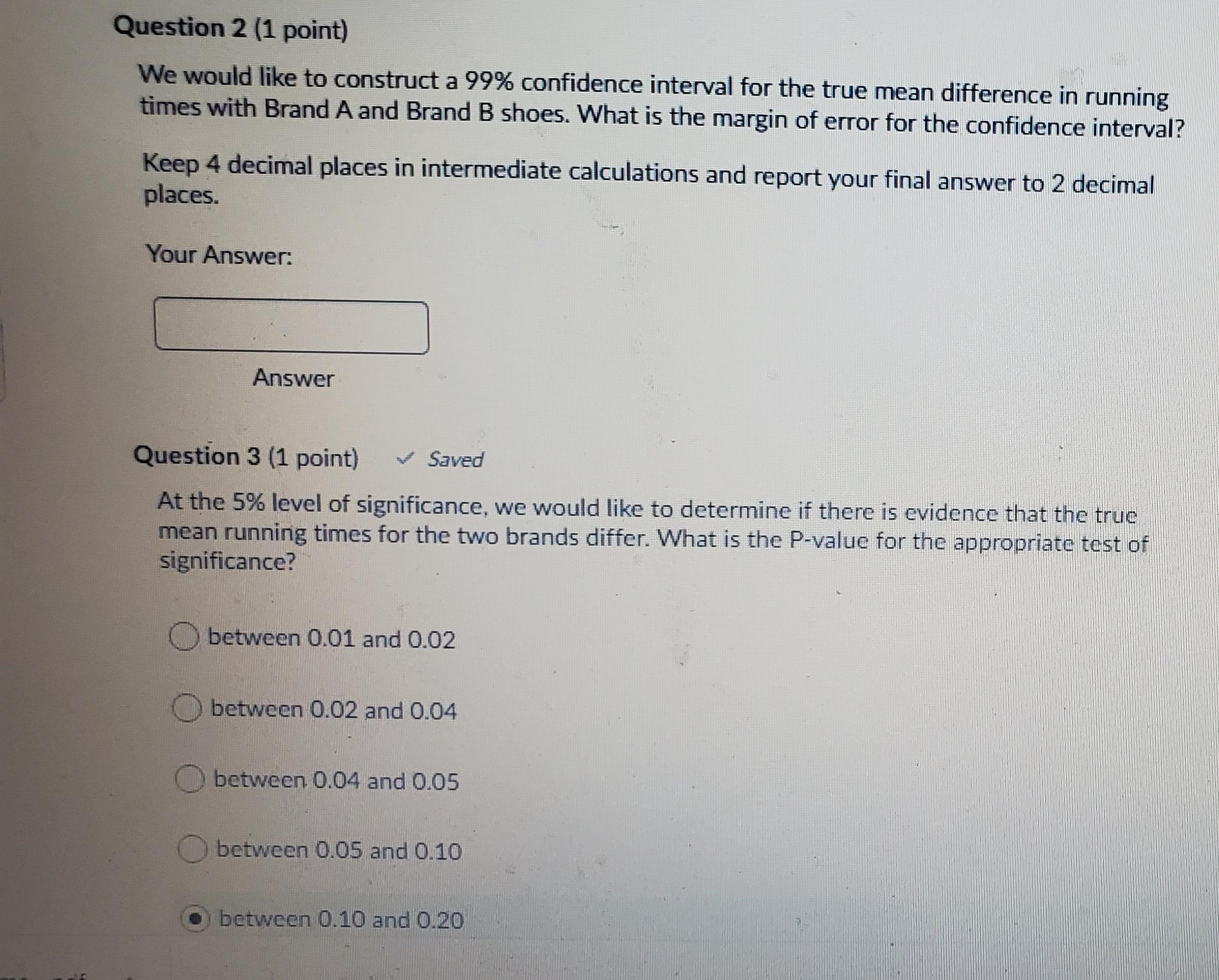
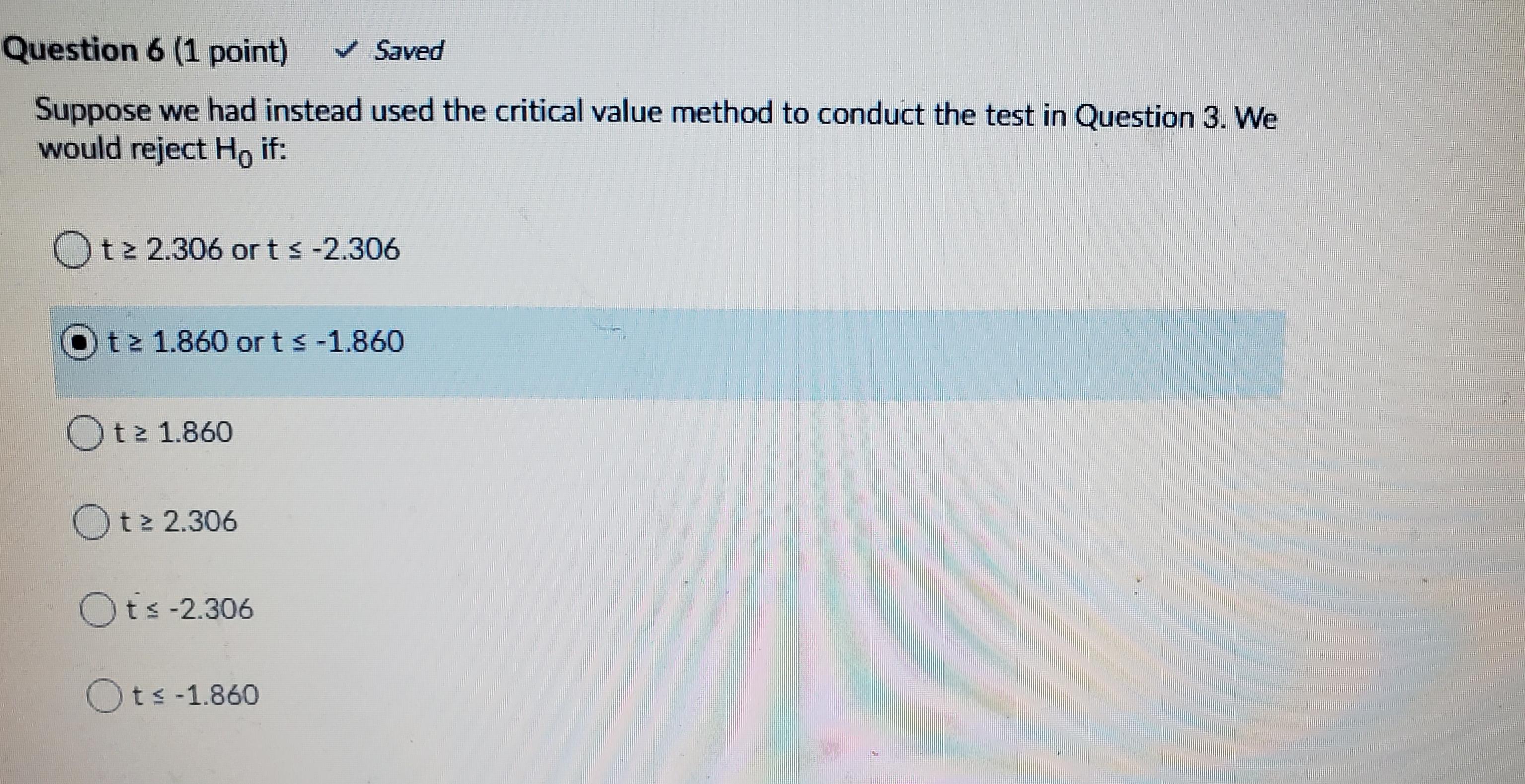
Transcribed Image Text:

Nine runners agree to participate in a study on two brands of shoes on the time to run a race. The runners are asked to run a 10-kilometer race on each of two consecutive weeks. In one of the races, the runners wear one brand of shoe and in the other a different brand (with the order randomly determined). The differences in running times (Brand A minus Brand B) have a mean of -0.27 minutes with a standard deviation of 0.4 minutes. Question 1 (1 point) V Saved Which of the following statements is/are true? (You must select all of the correct answer choices and none of the incorrect answer choices in order to receive credit. No partial credit will be given.) In order to conduct a matched pairs t test, we must assume that differentes in running times are normally distributed. In order to conduct a matched pairs t test, we must assume that running times with Brand A shoc and Brand B shoe arc both normally distributed. For any two runners, running times with Brand A shoc are independent. For cach runner, running times with Brand A shoc and Brand B shoc are independent. Question 2 (1 point) We would like to construct a 99% confidence interval for the true mean difference in running times with Brand A and Brand B shoes. WWhat is the margin of error for the confidence interval? Keep 4 decimal places in intermediate calculations and report your final answer to 2 decimal places. Your Answer: Answer Question 3 (1 point) v Saved At the 5% level of significance, we would like to determine if there is evidence that the true mean running times for the two brands differ. What is the P-value for the appropriate test of significance? between 0.01 and 0.02 between 0.02 and 0.04 between 0.04 and 0.05 between 0.05 and 0.10 between 0.10 and 0.20 Question 4 (1 point) What is the interpretation of the P-value in the previous question? O A) If the true mean running time were equal for the two brands, the probability of incorrectly concluding that the means differ would be (your answer to previous question). O B) The probability that the true mean running time differs for the two brands is (your answer to previous question). C) If the true mean running time were equal for the two brands, the probability of observing a sample mean of differences at least as cxtreme as -0.27 would be (your answer to previous question). D) The probability that the true mean running time is equal for the two brands is (your answer to previous question). O E) If the true mean running time differed for the two brands, the probability of observing a sample mean of differences at least as extreme as -0.27 would be (your answer to previous question). Question 5 (1 point) V Saved We will commit a Type II error in the hypothesis test in Question 3 if we conclude that there is: O A) sufficient evidence that average running times for the two brands differ when in fact average running times for the two brands do differ. O B) insufficient evidence that average running times for the two brands differ when in fact average running times for the two brands do differ. O C) sufficient evidence that there is no difference in average running times for the two brands when in fact average running times for the two brands do differ. O D) sufficient evidence that average running times for the two brands differ when in fact there is no difference in average running times for the two brands. E) insufficient evidence that there is no difference in average running times for the two brands when in fact average running times for the two brands do differ. OF) insufficient evidence that there is no difference in average running times for the two brands when in fact there is no difference in average running times for the two brands. G) sufficient evidence that there is no difference in average running times for the two brands when in fact there is no difference in average running times for the two brands. H) insufficient evidence that average running times for the two brands differ when in fact there is no difference in average running times for the two brands. Question 6 (1 point) V Saved Suppose we had instead used the critical value method to conduct the test in Question 3. We would reject Ho if: Otz 2.306 orts-2.306 Otz 1.860 or t s-1.860 Otz 1.860 Ot2 2.306 Ots-2.306 Ots-1.860 Nine runners agree to participate in a study on two brands of shoes on the time to run a race. The runners are asked to run a 10-kilometer race on each of two consecutive weeks. In one of the races, the runners wear one brand of shoe and in the other a different brand (with the order randomly determined). The differences in running times (Brand A minus Brand B) have a mean of -0.27 minutes with a standard deviation of 0.4 minutes. Question 1 (1 point) V Saved Which of the following statements is/are true? (You must select all of the correct answer choices and none of the incorrect answer choices in order to receive credit. No partial credit will be given.) In order to conduct a matched pairs t test, we must assume that differentes in running times are normally distributed. In order to conduct a matched pairs t test, we must assume that running times with Brand A shoc and Brand B shoe arc both normally distributed. For any two runners, running times with Brand A shoc are independent. For cach runner, running times with Brand A shoc and Brand B shoc are independent. Question 2 (1 point) We would like to construct a 99% confidence interval for the true mean difference in running times with Brand A and Brand B shoes. WWhat is the margin of error for the confidence interval? Keep 4 decimal places in intermediate calculations and report your final answer to 2 decimal places. Your Answer: Answer Question 3 (1 point) v Saved At the 5% level of significance, we would like to determine if there is evidence that the true mean running times for the two brands differ. What is the P-value for the appropriate test of significance? between 0.01 and 0.02 between 0.02 and 0.04 between 0.04 and 0.05 between 0.05 and 0.10 between 0.10 and 0.20 Question 4 (1 point) What is the interpretation of the P-value in the previous question? O A) If the true mean running time were equal for the two brands, the probability of incorrectly concluding that the means differ would be (your answer to previous question). O B) The probability that the true mean running time differs for the two brands is (your answer to previous question). C) If the true mean running time were equal for the two brands, the probability of observing a sample mean of differences at least as cxtreme as -0.27 would be (your answer to previous question). D) The probability that the true mean running time is equal for the two brands is (your answer to previous question). O E) If the true mean running time differed for the two brands, the probability of observing a sample mean of differences at least as extreme as -0.27 would be (your answer to previous question). Question 5 (1 point) V Saved We will commit a Type II error in the hypothesis test in Question 3 if we conclude that there is: O A) sufficient evidence that average running times for the two brands differ when in fact average running times for the two brands do differ. O B) insufficient evidence that average running times for the two brands differ when in fact average running times for the two brands do differ. O C) sufficient evidence that there is no difference in average running times for the two brands when in fact average running times for the two brands do differ. O D) sufficient evidence that average running times for the two brands differ when in fact there is no difference in average running times for the two brands. E) insufficient evidence that there is no difference in average running times for the two brands when in fact average running times for the two brands do differ. OF) insufficient evidence that there is no difference in average running times for the two brands when in fact there is no difference in average running times for the two brands. G) sufficient evidence that there is no difference in average running times for the two brands when in fact there is no difference in average running times for the two brands. H) insufficient evidence that average running times for the two brands differ when in fact there is no difference in average running times for the two brands. Question 6 (1 point) V Saved Suppose we had instead used the critical value method to conduct the test in Question 3. We would reject Ho if: Otz 2.306 orts-2.306 Otz 1.860 or t s-1.860 Otz 1.860 Ot2 2.306 Ots-2.306 Ots-1.860

Answer rating: 100% (QA)

1Option A and D are true dependent samples 2paired t in... View the full answer