There is a lottery with n coupons and n people take part in it. Each person picks exactly one coupon. Coupons are numbered consecutively from 1 to n, n being the maximum ticket number. The winner of the lottery

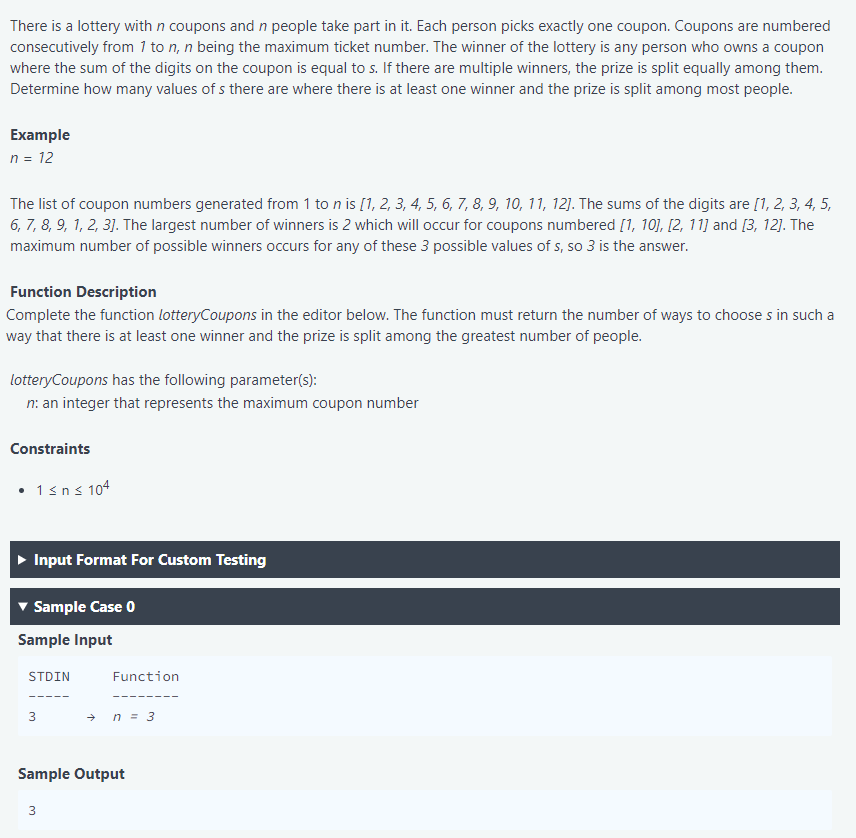
Transcribed Image Text:

There is a lottery with n coupons and n people take part in it. Each person picks exactly one coupon. Coupons are numbered consecutively from 1 to n, n being the maximum ticket number. The winner of the lottery is any person who owns a coupon where the sum of the digits on the coupon is equal to s. If there are multiple winners, the prize is split equally among them. Determine how many values of s there are where there is at least one winner and the prize is split among most people. Example n = 12 The list of coupon numbers generated from 1 to n is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]. The sums of the digits are [1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3]. The largest number of winners is 2 which will occur for coupons numbered [1, 10], [2, 11] and [3, 12]. The maximum number of possible winners occurs for any of these 3 possible values of s, so 3 is the answer. Function Description Complete the function lotteryCoupons in the editor below. The function must return the number of ways to choose s in such a way that there is at least one winner and the prize is split among the greatest number of people. lotteryCoupons has the following parameter(s): n: an integer that represents the maximum coupon number Constraints • 1 ≤ n ≤ 104 Input Format For Custom Testing Sample Case 0 Sample Input STDIN ‒‒‒‒‒ 3 Function w ‒‒‒‒‒‒ → n = 3 Sample Output There is a lottery with n coupons and n people take part in it. Each person picks exactly one coupon. Coupons are numbered consecutively from 1 to n, n being the maximum ticket number. The winner of the lottery is any person who owns a coupon where the sum of the digits on the coupon is equal to s. If there are multiple winners, the prize is split equally among them. Determine how many values of s there are where there is at least one winner and the prize is split among most people. Example n = 12 The list of coupon numbers generated from 1 to n is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]. The sums of the digits are [1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3]. The largest number of winners is 2 which will occur for coupons numbered [1, 10], [2, 11] and [3, 12]. The maximum number of possible winners occurs for any of these 3 possible values of s, so 3 is the answer. Function Description Complete the function lotteryCoupons in the editor below. The function must return the number of ways to choose s in such a way that there is at least one winner and the prize is split among the greatest number of people. lotteryCoupons has the following parameter(s): n: an integer that represents the maximum coupon number Constraints • 1 ≤ n ≤ 104 Input Format For Custom Testing Sample Case 0 Sample Input STDIN ‒‒‒‒‒ 3 Function w ‒‒‒‒‒‒ → n = 3 Sample Output There is a lottery with n coupons and n people take part in it. Each person picks exactly one coupon. Coupons are numbered consecutively from 1 to n, n being the maximum ticket number. The winner of the lottery is any person who owns a coupon where the sum of the digits on the coupon is equal to s. If there are multiple winners, the prize is split equally among them. Determine how many values of s there are where there is at least one winner and the prize is split among most people. Example n = 12 The list of coupon numbers generated from 1 to n is [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]. The sums of the digits are [1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3]. The largest number of winners is 2 which will occur for coupons numbered [1, 10], [2, 11] and [3, 12]. The maximum number of possible winners occurs for any of these 3 possible values of s, so 3 is the answer. Function Description Complete the function lotteryCoupons in the editor below. The function must return the number of ways to choose s in such a way that there is at least one winner and the prize is split among the greatest number of people. lotteryCoupons has the following parameter(s): n: an integer that represents the maximum coupon number Constraints • 1 ≤ n ≤ 104 Input Format For Custom Testing Sample Case 0 Sample Input STDIN ‒‒‒‒‒ 3 Function w ‒‒‒‒‒‒ → n = 3 Sample Output

• Expert Answer

Code is in View the full answer