How many 13C signals would the following molecule give? 0 . 2 3 4 5 H...
Fantastic news! We've Found the answer you've been seeking!
Question:
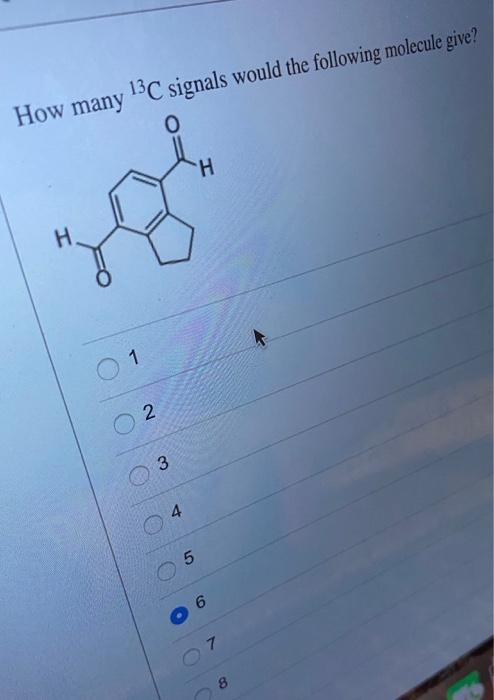
Transcribed Image Text:
How many 13C signals would the following molecule give? 0 Н. 2 3 4 5 H 6 07 8 How many 13C signals would the following molecule give? 0 Н. 2 3 4 5 H 6 07 8
Expert Answer:
Related Book For 

Posted Date:
Students also viewed these finance questions
-
Two Cigar makers are trying to determine whether or not to advertize their products on TV, and the effect on their profits. The Govt. is likely to ban Advt. related to Smoking on TV, and would charge...
-
A $1,000 par value, 30 year bond is 5 years old. It pays interest once a year at an annually compounded coupon rate of 12%. The market is returning 8% on comparable bonds. What is the bond's market...
-
A Treasury bond that matures in 10 years has a yield of 6%. A 10-year corporate bond has a yield of 9%. Assume that the liquidity premium on the corporate bond is 0.5%. What is the default risk...
-
Single PlantwideandMultiple Production Department Factory Overhead Rate Methodsand Product Cost Distortion Eclipse Motor Company manufactures two types of specialty electric motors, a commercial...
-
What are the five properties of money?
-
Benford, Inc., is planning to open a new sporting goods store in a suburban mall. Benford will lease the needed space in the mall. Equipment and fixtures for the store will cost $200,000 and be...
-
The Dow Jones Industrial Average is an average of the prices of 30 industrial stocks with equal weights applied to all 30 stocks (but the sum of the weights is greater than 1). Occasionally (about...
-
On January 1, the company issued 10-year bonds with a face value of $200,000. The bonds carry a coupon rate of 10%, and interest is paid semiannually. On the issue date, the market interest rate for...
-
Issue 2: The Manager Michael Scott is the regional manager at Dunder Mifflin Scranton, and therefore holds a formal leadership role. DM Corporate is unsure about Michael's effectiveness as a leader -...
-
The G. Saussy Manufacturing company is putting out four new electronic components. Each of Saussy's four plants has the capacity to add one more product to its current line of electronic parts. The...
-
How do consolidations and acquisitions (M&A) influence corporate money for a situation study, and what are the vital variables and contemplations that organizations ought to consider while taking...
-
Suzanne acquired the following ordinary shares in Quarine plc: She made no further acquisitions and the shares were valued at 3.20 each on 31 March 1982. On 24 July 2020, Suzanne sold 1,200 shares...
-
In May 2015, Ruth sold a freehold building which she had used exclusively for business purposes. The building was sold for 220,000, realising a chargeable gain of 42,500. In the following month, Ruth...
-
Select an agreement from Table 19.1 and investigate the details. For additional readings and websites pertaining to the material inthis chapter, see www.mhhe.com/field8e. Name of Agreement Marine...
-
Roseanne is a Scottish taxpayer. She starts trading on 1 July 2020 and prepares accounts for the 16 months to 31 October 2021. The adjusted trading profit for this period is 38,560. Her only other...
-
Joan has been a full-time director of Sunnybank Pursuits Ltd (a trading company) since 2001 and has owned 10% of the company's ordinary shares since 2002. She retired in February 2021 and gave all of...
-
Modern Designs Ltd. is considering opening up a new store in Perth. The store will have a life of 25 years. It will generate annual sales of 4,700 machines, and the price of each machine is $3,500....
-
Write a program to move a signed number from smaller register to bigger register. Hint: movzx ax, bl Topic: Data Related Operators and Directives in assembly language
-
The preceding problems can be solved using the interest tables supplied in Appendix A. To test your ability to construct your own interest factors or to use the computer programs available with this...
-
Putcall parity basically says that combination of a stock and a put produces the same return as the comparable position in a call and a risk-free bond. If not, at least one market is in...
-
1. What happens to the portfolio standard deviation as the investor substitutes the foreign securities for the U.S. securities? What combination of U.S. and Japanese stocks and U.S. and Brazilian...
-
Based upon the information in Exhibit 1, the market value added of the hypothetical firm is closest to: A. R 65 million. B. R 113 million. C. R 168 million. Mangoba Nkomo, CFA, a senior equity...
-
The most appropriate response to Nkomos Question 1 would be that the present value of future residual earnings is expected to be: A. zero. B. positive. C. negative. Mangoba Nkomo, CFA, a senior...
-
The most appropriate response to Nkomos Question 2 would be that the firms return on equity (ROE ) is: A. equal to the firms cost of equity. B. lower than the firms cost of equity. C. higher than the...

Study smarter with the SolutionInn App



