Refer to Exercise 11.66. Vuorinen fit the water outflow–time model for each of nine permeability–porosity combinations and used the results to develop a model for the coefficient of permeability of concrete, y. Specifically, he fit the model* 

E(y) = β_o + β₁x + β₂x₂

where 

x₁ = Porosity of the cement

x₂ = Estimated slope coefficient (α̂₁) of the corresponding water outflow–time regression line

The data are reproduced in the next table.

a. Find the least-squares prediction equation and interpret the β estimates.

b. Conduct a test of overall model utility. Interpret the p-value of the test.
c. Is there evidence that concrete porosity x₁ is a useful predictor of coefficient of permeability y? Test using α = .05.

d. Is there evidence that the estimated water outflow–time slope is a useful predictor of coefficient of permeability y? Test using α = .05.    

e. Find R² and interpret its value.

f. Find the estimate of s and interpret its value.

g. Find a 95% prediction interval for y when x₁ = .05 and x₂ = .30. Interpret the result.

Data from Exercise 11.66

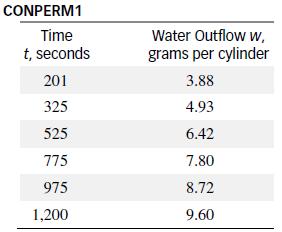
J. Vuorinen carried out a series of experiments to gather information on the coefficient of permeability of concrete (Magazine of Concrete Research, Sept. 1985). In one experiment, the outflow of water from the pores of a concrete specimen after it had been under saturating water pressure for a period of time was recorded for different combinations of concrete permeability and porosity. The resulting water quantities after different lapses of time for one permeability–porosity combination are given in the table.

Transcribed Image Text:

CONPERM2 coefficient of Estimated water Permeability y, (meters Outflow Time per second) x 10-l. Porosity x1 Slope Coefficient x2 1.00 .050 .903 1.00 .035 .722 1.00 .025 .590 .10 .050 345 .10 .035 .282 .10 .025 .233 .01 .050 .103 .01 .035 .091 .01 .025 .078