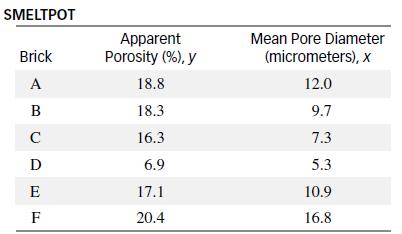
Refer to The American Ceramic Society Bulletin (Feb. 2005) study of aluminum smelter pots, Exercise 10.9. Recall that the life length of a smelter pot depends on the porosity of the brick lining. The apparent porosity of each of six brick specimens, as well as the mean pore diameter of each brick, is reproduced in the accompanying table. Use matrix algebra and the method of least–squares to fit the straight-line model E(y) = β_o + β₁x to the six data points.

a. Construct Y and X matrices for the data.

b. Find X'X and X'Y.

c. Verify that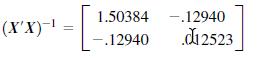

d. Find the β matrix, then give the least-squares prediction equation.

e. Find SSE and s².

f. Find the standard error of β̂₁.

g. Give and interpret a 90% confidence interval for β₁.

h. Find and interpret the value of R².

i. Give and interpret a 90% prediction interval for y when x = 10.

Data from Exercise 10.9

An investigation of the properties of bricks used to line aluminum smelter pots was published in The American Ceramic Society Bulletin (Feb. 2005). Six different commercial bricks were evaluated. The life length of a smelter pot depends on the porosity of the brick lining (the less porosity, the longer the life); consequently, the researchers measured the apparent porosity of each brick specimen, as well as the mean pore diameter of each brick.

Transcribed Image Text:

SMELTPOT Mean Pore Diameter Apparent Porosity (%), y Brick (micrometers), x A 18.8 12.0 В 18.3 9.7 16.3 7.3 D 6.9 5.3 E 17.1 10.9 F 20.4 16.8