Refer to the U.S. Army Corps of Engineers data on fish contaminated from the toxic discharges of a chemical plant located on the banks of the Tennessee River in Alabama. Recall that the engineers measured the length (in centimeters), weight (in grams), and DDT level (in parts per million) for 144 captured fish. In addition, the number of miles upstream from the river was recorded. The data are saved in the DDT file. 

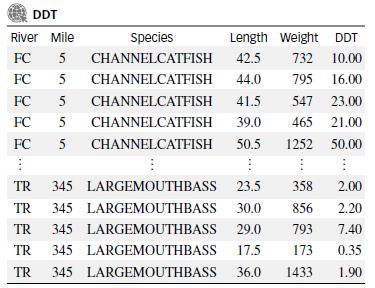
a. Fit the first-order model, E(y) = β_o + β₁x₁ + β₂x₂ + β₃x₃ to the data, where y = DDT level, x₁ = mile, x₂ = length, and x₃ = weight. Report the least-squares prediction equation.

b. Find the estimate of the standard deviation of ∈ for the model and give a practical interpretation of its value.

c. Do the data provide sufficient evidence to conclude that DDT level increases as length increases? Report the observed significance level of the test and reach a conclusion using α = .05.

d. Find and interpret a 95% confidence interval for β₃.

e. Test the overall adequacy of the model using α = .05.

f. Predict, with 95% confidence, the DDT level of a fish caught 100 miles upstream with a length of 40 cm and a weight of 800 g. Interpret the result.

Transcribed Image Text:

DDT River Mile species Length weight DDT FC 5 CHANNELCATFISH 42.5 732 10.00 FC 5 CHANNELCATFISH 44.0 795 16.00 FC 5 CHANNELCATFISH 41.5 547 23.00 FC CHANNELCATFISH 39.0 465 21.00 FC CHANNELCATFISH 50.5 1252 50.00 TR 345 LARGEMOUTHBASS 23.5 358 2.00 TR 345 LARGEMOUTHBASS 30.0 856 2.20 TR 345 LARGEMOUTHBASS 29.0 793 7.40 TR 345 LARGEMOUTHBASS 17.5 173 0.35 TR 345 LARGEMOUTHBASS 36.0 1433 1.90 in