Since o , 1 , k are independent of s 2 , it follows that l a o o a 1 1 a k k is independent of s 2 Use this fact and Theorems 11 2 and 11 3 to show that has a Students T distribution with n (k 1) degrees of freedom e E() T sVa' (X'X)a...

The Answer is in the image, click to view ...

Since o , 1 , ... k are independent of s 2 , it

Question:

Since β̂_o, β̂₁, ... β̂_k are independent of s², it follows that

l = a_oβ̂_o + a₁β̂₁ + ...... + a_kβ̂_k

is independent of s². Use this fact and Theorems 11.2 and 11.3 to show that

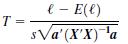has a Student’s T distribution with [n - (k + 1)] degrees of freedom.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Statistics For Engineering And The Sciences

ISBN: 9781498728850

6th Edition

Authors: William M. Mendenhall, Terry L. Sincich

See More Books

Question Posted: Apr 30, 2021 01:36 AM

See More Questions

Use limit theorems to show that the following functions are continuous on [0,1]. a) b) c) d) sin x cos x x +x-2 x#1 2 0 f(x) = 0
Show that if n and k are integers with 1 ¤ k ¤ n, then
Show that the F distribution with 4 and 4 degrees of freedom is given by And use this density to find the probability that for independent random samples of size n = 5 from normal populations with...
Write a function named "count the" in C which counts the number of times a given word "the" appears in the string parameter. Test Data: Input: The string where the word the present more than once....
Refer to Figure 7.1.4a, and suppose that p1 - p2 = 10 lb/in.2, A = 3 in.2, and mg = 600 lb. If the mass starts from rest at x(0) = 0, how far will it move in 0.5 sec, and how much hydraulic fluid...
Raj Trading reported the following amounts in its financial statements: In making the physical count of inventory, the following errors were made: (1) Inventory on Dec. 31, 2014: included $25,000 of...
Monroe Bradstad borrowed $$100,000$ from his aunt, Jeanne Garland, to purchase farmland. Both parties subsequently signed a promissory note stipulating that interest would be accrued prior to or on...
Thaarugo, Inc., produces a GPS device that is becoming popular in parts of Scandinavia. When Thaarugo produces one of these, a printed circuit board (PCB) is used, and it is populated with several...
Amazon, Inc. Presentation Your chief executive officer (CEO) has asked you to present the company's (Amazon, Inc.) process on making decisions under risks and uncertainty at the annual shareholders'...
Plot the following data and determine the preconsolidation pressure and the modified compression index. Specimen height is 25.4 mm, wn = 32.5%, d = 1.45 Mg/m3. Sample is from a depth of -11.5 m. %...
Let l = y = o , + 1 x 1 + 2 x 2 , ... k x k . Use the T statistic of Exercise 11.13, in conjunction with the pivotal method, to derive the formula for a (1 - )100% confidence interval for E(y).
Zoning is defined as the distribution of vacant land to residential and nonresidential uses via policy set by local governments. Although the negative effects of zoning have been studied (e.g.,...
The operating costs per trip of bus services and their mean fares, both in dollars, are shown in Table 14 for some randomly selected fixed-route bus services. Let C be the operating cost per trip and...
Question 5 Consider a firm that is a monopolist and sells in two distinct markets. The demand curves in the two markets are: P1 = 160 -8Q1 P2 = 80-2Q2 The marginal cost curves is 5+ Q where Q is the...
List and explain the experiments and observations show that light behaves as a particle.
Consider a closed container at equilibrium filled with water, argon and helium at 75C and 2x10 Pa. The number of moles of argon and helium in the vapor are equal. You can consider that the vapor is...
What is the role of Fire/EMS when there is an active "hot zone" event with law enforcement in command? In other words, the danger is not considered over? What should Fire/EMS be considering when...
Consider the IVP on [0, 1]: y = -y1 - Y2 y2 = Y1 - Y2 31(0) = 1,2(0)= = 0 (a) Verify that the solution is y1(t) = et cost, y2(t) = et sint. (b) Apply Euler's Method with step sizes h = 0.1 and 0.01...
In the microwave experiment of Example 25.1 and in the Michelson interferometer, we ignored phase changes due to reflection from a metal surface. Microwaves and light are inverted when they reflect...
Why do bars offer free peanuts?
The smooth uniform rod AB is supported by a ball-and-socket joint at A, the wall at B, and cable BC. Determine the components of reaction at A, the tension in the cable, and the normal reaction at B...
Determine the force in each member of the Pratt truss, and state if the members are in tension or compression. 2 m K. 2 m 2 m AG C E -2 m--2 m--2 m--2 m--2 m--2 m- |B 10 kN 10 kN 20 kN
Members AB and BC can each support a maximum compressive force of 800 lb, and members AD, DC, and BD can support a maximum tensile force of 1500 lb. If a = 10ft, determine the greatest load P the...
Financial ratios provide insight into a company's health but should be taken with a dose of skepticism. Debate the benefits and pitfalls of ratio analysis as a stand - alone analysis of a company's...
Line has equation r = (-5i + 10j+k) + (61-3j+ 2k) where 1 is a scalar. Line 2 has equation r = = (12i+14j5k)+(-i-2j+ 2k) where is a scalar. a) Show that lines I, and 12 meet, and find the coordinates...
Pursuant to a complete liquidation, EB Corporation distributes the following assets to its unrelated shareholders: land held for three years as an investment ( basis of $ 3 0 0 K , fair market value...

Since o , 1 , ... k are independent of s 2 , it

Question:

e - E(€) T = sVa' (X'X)a

Step by Step Answer:

Statistics For Engineering And The Sciences

Students also viewed these Engineering questions