(a) If the probability density of X is given by Find E(X), E(X 2 ), and E(X 3 ) (b) Use the results of part (a) to determine E( X 3 2X 2 3X 1) elsewhere...

(a) If the probability density of X is given by Find E(X), E(X 2 ), and E(X...

Question:

(a) If the probability density of X is given by

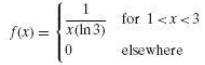
Find E(X), E(X²), and E(X³).

(b) Use the results of part (a) to determine E( X³ + 2X² - 3X + 1).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:05 AM

See More Questions

If the probability density of X is given by Check whether its mean and its variance exist. f 2x-3 for 1 elsewhere fx)-
Use the transformation technique to rework Exercise 7.2. In exercise If the probability density of X is given by And Y = X2 2xeforx0 0 elsewhere f(x) =
If the probability density of X is given by Where k is an appropriate constant, find the probability density of the random variable Y = 2X / 1+ 2X . Identify the distribution of Y, and thus determine...
X-Tech Inc. produces specialized bolts for the aerospace industry. The operating cost of producing a single bolt is $2. The company currently sells the bolts for $6/unit. Each time the company...
The full-time student body of a college is composed of 50% males and 50% females. Does a random sample of students (30 male, 20 female) from an introductory chemistry course show sufficient evidence...
Determine the force P needed to support the 100-lb weight. Each pulley has a weight of 10 lb. Also, what are the cord reactions at A andB? 2 in. 2 in. 2 in
Formally show that \[ D_{i}=\frac{r_{i}}{p} \frac{h_{i i}}{1-h_{i i}} \]
Scotty's Scooters plans to sell a standard scooter for $55 and a chrome scooter for $70. Scotty's purchases the standard scooter for $30 and the chrome scooter for $40. Scotty's expects to sell one...
Kramerica Industries has come up with an ingenious business plan. Kramerica has two divisions. The first division manufactures the most delicious ice cream in the world. One scoop of this ice cream...
Describe three high-contact service operations and three low-contact service operations. Do the concepts of intangibility and unstorability have different implications for low- and high-contact...
To illustrate the proof of Theorem 4.1, consider the random variable X, which takes on the values -2, -1, 0, 1, 2, and 3 with probabilities f (-2), f (-1), f (0), f (1), f (2), and f (3). If g(X) = X...
With reference to Exercise 3.47 on page 90, find E(2X Y).
Some firms products are so well known that the entire category of products offered in the industry (including rivals products) is often referred to by the leading firms brand name (which is called an...
Group performance does not depend on individual and collective efforts. True False
Which of these roles helps maintain participation and obligation to the group by the group members on an emotional level? Work roles Maintenance role Blocking role None of the above
Provide the definition of cost basis and adjusted basis and what is included to calculate basis.
Which of the following is a positive reaction to the barrier encountered in achieving a desired goal? Restructuring Withdrawal Fixation Regression
A cross-functional team comprises individuals with different functional proficiency. True False
A project has estimated annual net cash flows of $118,600. It is estimated to cost $616,720. Determine the cash payback period. Round to one decimal place.
The following processes constitute the air-standard Diesel cycle: 12: isentropic compression,23: constant-volume energy addition (T and P increase),34: constant-pressure energy addition (v...
The accounting department at Weston Materials Inc., a national manufacturer of unattached garages, reports that it takes two construction workers a mean of 32 hours and a standard deviation of 2...
A recent report indicated a typical family of four spends $490 per month on food. Assume the distribution of food expenditures for a family of four follows the normal distribution, with a standard...
A study of long-distance phone calls made from General Electric Corporate Headquarters in Fairfield, Connecticut, revealed the length of the calls, in minutes, follows the normal probability...
After the company issues an initial public offering and they desire to offer additional shares, one option is the seasoned equity offering. What are the differences between a convertible bond and a...
4. A stock provides a dividend yield of 5.0% paid semi- annually. The spot price of the stock is currently $500, and the risk-free rate is 7.5% with continuous compounding for all maturities. 1. What...
1. A 1000 bond issued on January 10, 2021 is paying coupons at a nominal interest rate of 7% payable semiannually. The bond is redeemed at par and matures on January 10, 2031. The nominal yield rate...

(a) If the probability density of X is given by Find E(X), E(X 2 ), and E(X...

Question:

elsewhere

Step by Step Answer:

a b 263ln 3 8ln 3 6ln ...View the full answer

John E Freunds Mathematical Statistics With Applications

Students also viewed these Statistics questions