To illustrate the proof of Theorem 4.1, consider the random variable X, which takes on the values

Question:

To illustrate the proof of Theorem 4.1, consider the random variable X, which takes on the values -2, -1, 0, 1, 2, and 3 with probabilities f (-2), f (-1), f (0), f (1), f (2), and f (3). If g(X) = X₂, find

(a) g₁, g₂, g₃, and g₄, the four possible values of g(x);

(b) the probabilities P[g(X) = g_i] for i = 1, 2, 3, 4;

(c)

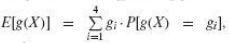
And show that it equals

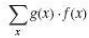
Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:05 AM

See More Questions

Carry out the details of the proof of Theorem 4.
Complete the proof of Theorem 4.38(a) by showing that if the recurrence relation x n = ax n-1 + bx n-2 has distinct eigenvalues 1 2 , then the solution will be of the form x n = c 1 n 1 + c 2 n 2
Does the proof of Theorem 2.2 fail to consider the possibility that the set of vectors is empty (i.e., that k = 0)?
1) Determine the pH of a 4.3*10^-4 M NaOH solution. 2) why would we say that a solution with a H+ concentration of 1.00*10^-7 M is said to be neutral if it contains acid, shouldn't be acidic?
A politician claims that she will receive 60% of the vote in an upcoming election. The results of a properly designed random sample of 100 voters showed that 50 of those sampled will vote for her. Is...
Determine the force P required to hold the 50-kg mass inequilibrium. B. P.
Table B. 14 contains data concerning the transient points of an electronic inverter. Fit a regression model to all 25 observations but only use $x_{1}-x_{4}$ as the regressors. Investigate this...
Mason Olson is chairman of the board of Healthy Fast Foods, Inc. Suppose Olson has just founded Healthy Fast Foods, and assume that he treats his home and other personal assets as part of Healthy...
Total debt-to-assets ratio, debt-to-equity ratio and Long-term debt-to-capital ratio are examples of what type or category of ratios?
The maintenance staff of a large office building regularly replaces fluorescent ceiling lights that have gone out. During a visit to a typical floor, the staff may have to replace several lights. The...
X is the number of heads and Y the number of heads minus the number of tails obtained in three flips of a balanced coin, construct a table showing the values of the joint probability distribution of...
(a) If the probability density of X is given by Find E(X), E(X 2 ), and E(X 3 ). (b) Use the results of part (a) to determine E( X 3 + 2X 2 - 3X + 1). elsewhere
Clouds consist of a. water droplets at all altitudes b. ice crystals at all altitudes c. water droplets at low altitudes and ice crystals at high altitudes d. ice crystals at low altitudes and water...
Operant conditioning theory of learning is used in educational research, control of alcoholism, and control of deviant children in a classroom. True False
When is an asset deemed long term for holding period purposes? Why is this important?
If each systolic reading is exactly twice the diastolic reading, what is the value of the linear correlation coefficient r?
Which of these is the loss of a persons individuality and tends to undertake activities as dictated by the mob or the group? Group size Groupthink Groupshift Deindividuation
A negative attitude is not responsible for creating mistrust among employees, whereas in a workplace with a positive attitude, inducing competitiveness is taken positively which inspires employees to...
A project has estimated annual net cash flows of $6,800 for five years and is estimated to cost $23,125. Assume a minimum acceptable rate of return of 12%. Using Exhibit 5, determine (1) the net...
Show that the block upper triangular matrix A in Example 5 is invertible if and only if both A 11 and A 22 are invertible. Data from in Example 5 EXAMPLE 5 A matrix of the form A = [ A11 A12 0 A22 is...
Many retail stores offer their own credit cards. At the time of the credit application, the customer is given a 10% discount on the purchase. The time required for the credit application process...
The time patrons at the Grande Dunes Hotel in the Bahamas spend waiting for an elevator follows a uniform distribution between 0 and 3.5 minutes. a. Show that the area under the curve is 1.00. b. How...
The net sales and the number of employees for aluminum fabricators with similar characteristics are organized into frequency distributions. Both are normally distributed. For the net sales, the mean...
Assume that a firm has weighted average cost of capital of 3.6% with a corporate tax rate of 21%. The pre-tax cost of debt is 3.1%. In case the firm would have no debt, the cost of equity for the...
Consider the stock of Aya Company, which will pay an annual dividend of $3 one year from today. The dividend will grow at a constant rate of 3%, forever.The market requires a 12% return on the...
Analyze the video presented on the link below. Also, please discuss or explain the video and relate it to personal finance. https://www.youtube.com/watch?v=nFY0HBkUm8o

To illustrate the proof of Theorem 4.1, consider the random variable X, which takes on the values

Question:

ー1

Step by Step Answer:

a 0 1 4 9 b hg 1 f 0 h...View the full answer

John E Freunds Mathematical Statistics With Applications

Students also viewed these Statistics questions