Differentiating with respect to the expressions on both sides of the equation Show that the mean

Question:

Differentiating with respect to θ the expressions on both sides of the equation

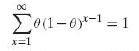
Show that the mean of the geometric distribution is given by µ = 1/θ. Then, differentiating again with respect to θ, show that µ'₂ = 2 – θ / θ² and hence that σ² = 1 – θ / θ².

Distribution
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...