If X 1 is the mean of a random sample of size n from a normal population
Question:
If X̅1 is the mean of a random sample of size n from a normal population with the mean µ and the variance σ21, X̅2 is the mean of a random sample of size n from a normal population with the mean µ and the variance σ22, and the two samples are independent, show that
(a) ω ∙ X̅1 +(1 – ω) ∙ X̅2, where 0 ≤ ω ≤ 1, is an unbiased estimator of µ;
(b) The variance of this estimator is a minimum when
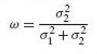
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

John E Freunds Mathematical Statistics With Applications
ISBN: 9780134995373
8th Edition
Authors: Irwin Miller, Marylees Miller
Question Posted:





