Let X 1 , X 2 , . . . , X n be a random sample
Question:
Let X1, X2, . . . , Xn be a random sample of size n from the uniform population given by
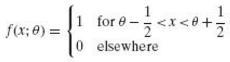
Show that if Y1 and Yn are the first and nth order statistic, any estimator Θ such that
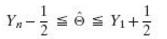
Can serve as a maximum likelihood estimator of θ. This shows that maximum likelihood estimators need not be unique.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Any value 61y 2 ...View the full answer
Answered By
Ajeet Singh
Hi there! Are you looking for a committed, reliable, and enthusiastic tutor? Well, teaching and learning are more of a second nature to me, having been raised by parents who are both teachers. I have done plenty of studying and lots of learning on many exciting and challenging topics. All these experiences have influenced my decision to take on the teaching role in various capacities. As a tutor, I am looking forward to getting to understand your needs and helping you achieve your academic goals. I'm highly flexible and contactable. I am available to work on short notice since I only prefer to work with very small and select groups of students. Areas of interest: Business, accounting, Project management, sociology, technology, computers, English, linguistics, media, philosophy, political science, statistics, data science, Excel, psychology, art, history, health education, gender studies, cultural studies, ethics, religion. I am also decent with math(s) & Programming. If you have a project you think I can take on, please feel welcome to invite me, and I'm going to check it out!
4+ Reviews
24+ Question Solved
Related Book For 
John E Freunds Mathematical Statistics With Applications
ISBN: 9780134995373
8th Edition
Authors: Irwin Miller, Marylees Miller
Question Posted:
