With reference to Exercise 10.72, check whether the following estimators are maximum likelihood estimators of : (a) 1/2 (Y 1 + Y n ); (b)

With reference to Exercise 10.72, check whether the following estimators are maximum likelihood estimators of θ:

(a) 1/2 (Y₁ + Y_n); 

(b) 1/3 (Y₁ + 2Y₂).

In exercise

Let X₁, X₂, . . . , X_n be a random sample of size n from the uniform population given by

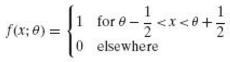
Show that if Y₁ and Y_n are the first and nth order statistic, any estimator Θ such that

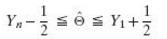
Can serve as a maximum likelihood estimator of θ. This shows that maximum likelihood estimators need not be unique.

f(x,e) = 0 elsewhere