If NKs do not distribute, you solve the Underwood Eq. (7-28) for (varphi), which satisfies (alpha_{mathrm{LK}-text {
Question:
If NKs do not distribute, you solve the Underwood Eq. (7-28) for \(\varphi\), which satisfies \(\alpha_{\mathrm{LK}-\text { ref }}>\varphi>\alpha_{\mathrm{HK}-\text { ref. }}\). However, if a different reference component is chosen for calculation of the relative volatilities, the value of \(\varphi\) changes. Despite the change in \(\varphi, \mathrm{V}_{\text {min }}\) calculated from Eq. (7-25a) is unchanged. The proof that this is true is challenging for the general case but is tractable for a binary system with a saturated liquid feed because Eq. (7-28) becomes linear. Prove for a binary system with a saturated liquid feed that the solution for \(\mathrm{V}_{\text {min }}\) is not affected by the choice of reference component for relative volatilities.
Question (7-25a) and (7-28)
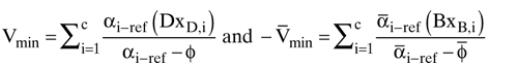
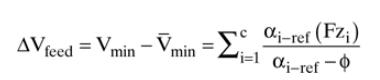
Step by Step Answer:

Separation Process Engineering Includes Mass Transfer Analysis
ISBN: 9780137468041
5th Edition
Authors: Phillip Wankat





