The following LP problem admits a degenerate primal solution, that is, one of the basic (associated with basic vectors) components of the optimal solution is equal to zero. Given the following LP problem

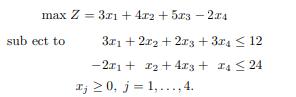
a) Solve the above problem using the appropriate algorithm and exhibit the primal optimal solution. (When you encounter a tie among minimum ratios, break it by ipping a coin.)

b) Exhibit the optimal primal and dual solutions.

c) Obtain another optimal dual solution and exhibit it. What algorithm did you use? Explain.

max Z=3x+4x2 + 523-224 sub ect to 3x1 +212 +213 +34 12 -2x1+2+4x3 + x424 x; 0, j=1,..., 4.